MagneticFields

For a special project of mine that will certainly revolution the entire world , I needed to understand basic Electro-Magnetism theory.

This page and the next deal with my encounters and difficulties but also with the results of my research.

Electro-Magnetism

Electro-Magnetism is a huge but absolutely necessary and fundamental domain in physics as it's the basis for most physical phenomena and study fields like optics, radio-astronomy, quantum physics, electronics, particles study, etc.

Electricity and magnetism were first seen as two distinct phenomena until the work of famous scientists like Ampère, Gauss, Faraday or Maxwell actually made the two inter-related. More than inter-related : actually inseparable from one another.

To test my Tex package, I'll list the 4 beautiful Maxwell equations (in stationary regime) that tie electricity and magnetism but also completely define them :

<math>\nabla \times \mathbf{H} = \mathbf{j}</math>	(1)
<math>\nabla \cdot \mathbf{B} = 0</math>	(2)
<math>\nabla \times \mathbf{E} = \mathbf{0}</math>	(3)
<math>\nabla \cdot \mathbf{D} = \rho_e</math>	(4)

where Boldface symbols are vectors, regular symbols are simple scalars and

<math>\mathbf{H}</math> is the magnetic field strength (or magnetic intensity) in <math>A.m^{-1}</math> (Ampère per mètre)

<math>\mathbf{B}</math> is the magnetic flux density (or magnetic induction) in <math>T</math> (Tesla)

<math>\mathbf{D}</math> is the electric flux density (or electric induction) in <math>C.m^{-2}</math> (Coulomb per square mètre)

<math>\mathbf{E}</math> is the electric field strength (or electric intensity) in <math>V.m^{-1}</math> (Volt per mètre)

<math>\mathbf{j}</math> is the free current density (that is, the current density related to the transport of free electric charges) in <math>A.m^{-2}</math> (Ampère per square mètre)

<math>\rho_e</math> is the volume density of free electric charges in <math>C.m^{-3}</math> (Coulomb per cubic mètre)

Notice the beautiful symmetry in these 4 equations. We will mostly leave the electric field equations aside in the following and concentrate on the magnetic field equations.

Typically, equations (1) and (2) simply mean that a magnetic field line always closes back to the emitter and that the net magnetic flux is always 0 as there is always the same amount that goes off from a surface that comes back into it, as stated in the following Gauss equation :

<math>\oint_S \mathbf{B} \cdot dA = 0</math> (for a closed surface)

Two Cases to Distinguish

As always, physics manuals are great if you already understand what the guy is talking about. Also, they always use the examples of solenoids with a current and a given number of coils whereas, although I knew electric current and magnetic fields are always strongly related, I needed a book that took me to the origins : permanent magnets.

After quite a long research I came out with some knowledge that I mainly gathered from an old book from 1942 simply called "Cours de Physique pour les classes de Mathématiques Spéciales" (Physics Course for Special Mathematics classes) by M. Joyal. This book is awesome ! It explains everything with clean drawings and I can't quite figure out why no one ever writes books like these anymore.

Anyway, there was a key equation that was always driving me mad as the terms were changing on and on, I'm speaking of :

<math>\mathbf{B}=\mu_0(\mathbf{H} + \mathbf{M})</math>

(5)

with <math>\mathbf{M}</math> (sometimes also called <math>\mathbf{J}</math>) is the magnetic polarization vector (or more generally, the magnetization of a medium) in <math>A.m^{-1}</math> (Ampère per mètre)

<math>\mathbf{M}</math> is a quantity that exists only inside magnetic materials (magnets, current loops or magnetized media like iron) and it can take various forms, hence the constant change in formulas that was bothering me.

Indeed, you can distinguish 2 cases:

1. Permanent Magnets, where <math>\mathbf{M}</math> is actually "generated" from the magnet as the statistic macroscopic sum of all the small microscopic dipoles <math>d\mathbf{M}</math>
2. Magnetic Materials, where <math>\mathbf{M}</math> is actually induced by the external magnetic field in which the material is set. In that case, <math>\mathbf{M}</math> is then a factor of <math>\mathbf{H}</math>, the external field, but also generates itself a new <math>\mathbf{H'}</math> coming from its own magnetization.

Permanent Magnets

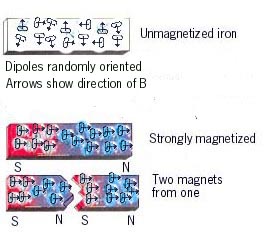
You can see permanent magnets as a more or less uniform assembly of atomic dipoles, each dipole carrying a small magnetic moment <math>d\mathbf{M}</math> that is responsible for rotating the dipole in the axis of any external field. An atomic dipole can be naively thought of as an electron orbiting about its atomic structure and creating a small current loop responsible for a tiny magnetic moment <math>d\mathbf{M}</math> as shown on the figure below :

The small current loops sort of cancel out each other inside the material only to leave surface dipoles which are the most active at the north and south poles of the magnets. These 2 oriented poles are resulting from the statistic sum of the orientation of each microscopic dipoles, finally yielding the global macroscopic dipole moment <math>\mathbf{M}</math>.

Magnetized Materials

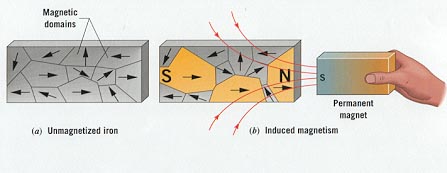
Materials susceptible to magnetism see their <math>\mathbf{M}</math> magnetic moment induced by any external field they are set into. This external field can be generated by permanent magnets, electro-magnets (solenoid coils) or even other magnetized materials (since permanent magnets are, after all, strongly magnetized materials themselves).

The figure below shows the process of induced magnetism by an external field, something we all could experience as a kid when playing with magnets :

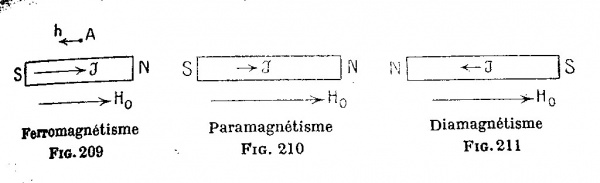
The "magnetizability" of a material is called its magnetic susceptibility <math>\chi</math> and we can write <math>\mathbf{M}=\chi\mathbf{H}</math> that shows how the "internal magnetization" <math>\mathbf{M}</math> is induced by the external field <math>\mathbf{H}</math> via the <math>\chi</math> factor. There are 3 classes of susceptible materials :

• Paramagnetic materials, which have a very low (e.g. <math>10^{-4}</math>) and positive susceptibility (thus generating a very low <math>\mathbf{M}</math> in the same direction as <math>\mathbf{H}</math>)
• Diamagnetic materials, which have a very low (e.g. <math>-10^{-4}</math>) and negative susceptibility (thus generating a very low <math>\mathbf{M}</math> in the opposite direction as <math>\mathbf{H}</math>)
• Ferromagnetic materials, which have a very high (e.g. <math>10^{3}</math>) and positive susceptibility (thus generating a very high <math>\mathbf{M}</math> in the same direction as <math>\mathbf{H}</math>)

The figure below shows a representation of the 3 types of materials and their induced internal field <math>\mathbf{M}</math> (or <math>\mathbf{J}</math> here) :

Merging Vectors

We saw 3 different types of vectors : <math>\mathbf{B}</math>, <math>\mathbf{H}</math> and <math>\mathbf{M}</math>.

<math>\mathbf{H}</math> and <math>\mathbf{M}</math> are both discontinuous fields as <math>\mathbf{H}</math> can be decomposed as the external and internal fields <math>\mathbf{H_e}</math> and <math>\mathbf{H_i}</math> and <math>\mathbf{M}</math> exists only inside a magnetic material and is <math>\mathbf{0}</math> outside.

Note that the internal field <math>\mathbf{H_i}</math> is produced by the induced internal field <math>\mathbf{M}</math> and is called the demagnetizing field that is defined as <math>\mathbf{H_i}=k\mathbf{M}</math> where <math>k</math> is the demagnetizing factor and is uniquely defined by the geometry of the piece of material (e.g. it's <math>-1/3</math> for a sphere).

So in general, inside a material we have : <math>\mathbf{B_i}=\mu_0(\mathbf{H_i} + \mathbf{M})</math>

And outside a material we have : <math>\mathbf{B_e}=\mu_0\mathbf{H_e}</math>

The advantage of using <math>\mathbf{B}</math> as being the sum of <math>\mathbf{H}</math> and <math>\mathbf{M}</math> is that, although <math>\mathbf{H}</math> and <math>\mathbf{M}</math> are discontinuous taken separately, <math>\mathbf{B}</math> is continuous through the entire space and also is what instruments usually measure as being the magnetic field.

In Practice

After this short summary, let's get back one of the aspects of the project : simulating the flux density <math>\mathbf{B}</math> in a 2D slab containing permanent magnets so we can compute the forces that the magnets exert on each other.

I bought a nice and cheap software called Vizimag developped by John Stuart Beeteson, a retired engineer from IBM. This was exactly what I needed to create as a software !

Why did I need to rewrite the software rather than using the existing Vizimag application ? Simply because I needed to integrate the computed forces over time to simulate motion. Also because although I was focusing on simulating forces in a 2D plane, I needed to be able to simulate multiple 2D planes working altogether (i.e. planes were inter-dependent). And finally, because magnetic flux density and the forces induced by them were merely one of the cogs in the larger application I needed to build : an application that was able to simulate relative motion of groups of magnets (some static, others in motion) and tell me whether a given magnets configuration was viable or not, and to perform adjustments to the configuration parameters in order to achieve viability.

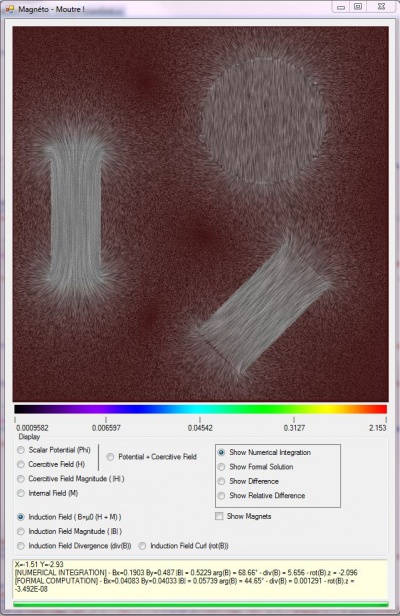
So I started to take some formulas and write a small application to simulate magnetic fields coming out from magnets from which you can see some results in the images below :

:::

All was going well until I started to simulate induced magnetic fields in arbitrary materials. The integrals I needed to solve soon became a nightmare. Also, as I was using Vizimag to check out my results, I realized that Vizimag was almost independent on the amount of magnets or materials you could put in the simulation. That's how I knew Mr Beeteson was solving his problem on a fixed grid and that only his grid's resolution mattered in the solving time, not the amount of items.

Quite disappointed for not using the correct approach, and quite discouraged from learning the overkill finite element/boundary methods for solving my problem, I went back to the university library and with the most incredible luck, I made a great discovery : I found the book "Visualizing Magnetic Fields" by... John Stuart Beeteson ! The guy wrote a book ! And he didn't even tell about it !

I borrowed the book and after careful reading, I saw it explained everything about Vizimag and even contained the "source code" of the most important parts.

What's Next Then ?

Let's see where it led me in Magnetic Fields (Part 2)