I wanted to write a short explanation about bitonic sort because it's simple as hell but no one does a good job at explaining it correctly.
You can find the video explanation here https://www.youtube.com/watch?v=GEQ8y26blEY but it's a bit tedious so to sum up the algorithm, here's what you need to know:
- A bitonic sequence is a sequence of numbers that can be ordered as first ascending then descending (or the opposite)
- For example: (1, 2, 3, 4) followed by (4,3,2,1) is bitonic.
- The bitonic sort algorithm works in 2 parts:
- (1) First, you need to transform any random sequence of numbers into a bitonic sequence
- (2) Second, you can then sort the bitonic sequence in ascending order
And that is all there is to it! Now let's see how to execute the 2 parts of the algorithm.
Contents
Quick Algorithm
Part 1: Transforming any sequence of numbers into a bitonic sequence
It's a O(N*log²(N)) algorithm where we recursively compare and swap elements 2 by 2 in a very specific manner.
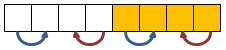
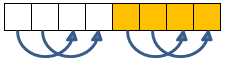
For 8 values, we first perform 4 compare&swaps like this (pass 1):
Then we perform 4 compares&swaps like this (pass 2):
Finally we perform 4 compares&swaps like this (pass 3):
Part 2: Sorting the bitonic sequence
Well it's another O(N*log²(N)) algorithm as in part 1. You'll need to swap numbers log2(N) times.
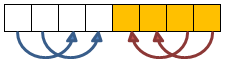
For 8 values, we first perform 4 compares&swaps like this (pass 1):
Then we perform 4 compares&swaps like this (pass 2):
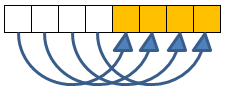
Finally we perform 4 compares&swaps like this (pass 3):
Example
Here x0, x1, ..., xn}+ describes a set of values in ascending order and {x0, x1, ..., xn}- describes a set of values in descending order. While { {...}+, {...}- }B describes a bitonic sequence.
Part 1
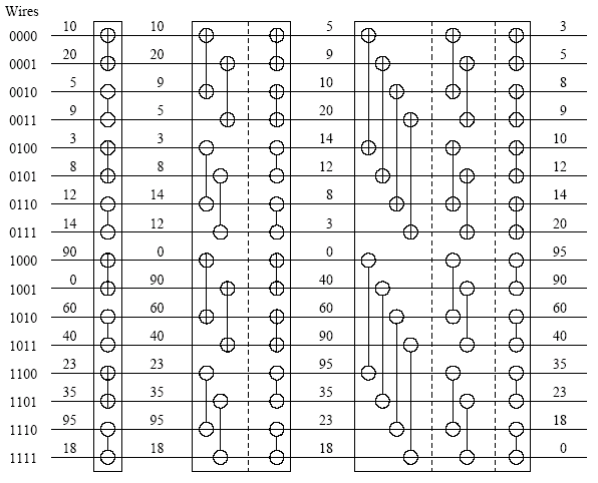
Initial random sequence: 35, 16, 31, 4, 4, 16, 17, 12
- Pass 1: {{16, 35}+, {31, 4}-}B, {{4, 16}+, {17, 12}-}B ← We already have 2 size 4 bitonic sequences
- Pass 2: 16, 4, 31, 35, 17, 16, 4, 12 ← It's becoming somewhat random again while we're sorting the 2 size 4 bitonic sequences into a single size 8 sequence
- Pass 3: {{4, 16, 31, 35}+, {17, 16, 12, 4}-}B ← And we're done!
Part 2
Initial bitonic sequence from part 1: 4, 16, 31, 35, 17, 16, 12, 4
- Pass 1: 4, 16, 12, 4, 17, 16, 31, 35
- Pass 2: 4, 4, 12, 16, 17, 16, 31, 35
- Pass 3: 4, 4, 12, 16, 16, 17, 31, 35 ← And we're done!
More about it
Part 1
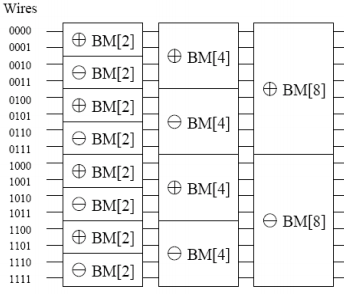
This is a nice graph explaining what's happening when building the initial bitonic sequence:
We can see there are 3 stages for N=16 possible values to sort (log2(N)-1).
- 1st stage consists of:
- 8 groups of one length-1 compares&swaps (C&S). Even groups are in ascending order, odd groups are in descending order.
- 2nd stage consists of:
- 4 groups of two length-2 C&S. Even groups are in ascending order, odd groups are in descending order.
- 4 groups of two length-1 C&S. Even groups are in ascending order, odd groups are in descending order.
- 3rd stage consists of:
- 2 groups of four length-4 C&S. Even groups are in ascending order, odd groups are in descending order.
- 2 groups of four length-2 C&S. Even groups are in ascending order, odd groups are in descending order.
- 2 groups of four length-1 C&S. Even groups are in ascending order, odd groups are in descending order.
In total, there are 8 + (8+8) + (8+8+8) possible compare&swaps or N + (2*N) + (3*N) + ... + (log(N)*N) = (log(N)*(log(N)+1) * N / 2) operations hence the O(N log²N) notation.