Color Spaces

A color space is the 3-dimensional space in which colors can be represented. 3 dimensions are enough for all applications to describe a color faithfully, but various conventions can be chosen to select each dimension depending on the intended goal (processing, display, accuracy, perception, etc.).

Some of the color spaces are CIE XYZ, CIE xyY, RGB, CIELAB, HSV, HSB, HSL, YUV.

CIE XYZ

The CIE 1931 XYZ color space should be considered the master color space as it can encompass and describe all other color spaces. It's also independent of any device and is a reference space.

You should check that very educational video for a visual explanation of what is XYZ as opposed to standard RGB : http://www.youtube.com/watch?v=x0-qoXOCOow

The human eye has photoreceptors (called cone cells) for medium- and high-brightness color vision, with sensitivity peaks in short (S, 420–440 nm), middle (M, 530–540 nm), and long (L, 560–580 nm) wavelengths.

In the CIE XYZ color space, the tristimulus values are not the S, M, and L responses of the human eye, but rather a set of tristimulus values called X, Y, and Z, which are roughly red, green and blue, respectively (note that the X,Y,Z values are not physically observed red, green, blue colors. Rather, they may be thought of as 'derived' parameters from the red, green, blue colors).

CIE xyY

The CIE 1931 color space chromaticity diagram. The outer curved boundary is the spectral (or monochromatic) locus, with wavelengths shown in nanometers. Note that the image itself describes colors using sRGB, and colors outside the sRGB gamut cannot be displayed properly. Depending on the color space and calibration of your display device, the sRGB colors may not be displayed properly either. This diagram displays the maximallly saturated bright colors that can be produced by a computer monitor or television set. (Source)

All around this compendium, you will find many images that look like the thumbnail to the right.

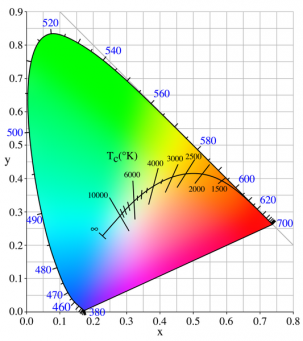
This is called the chromaticity diagram and is represented in the xyY color space, not to be confused with the XYZ color space seen above, although both are tightly related through simple linear transforms.

The concept of color can be divided into two parts: brightness (or luminance) and chromaticity. For example, the color white is a bright color, while the color grey is considered to be a less bright version of that same white. In other words, the chromaticity of white and grey are the same while their brightness differs.

The CIE XYZ color space was deliberately designed so that the Y parameter was a measure of the brightness or luminance of a color. The chromaticity of a color was then specified by the two derived parameters x and y, two of the three normalized values which are functions of all three tristimulus values X, Y, and Z:

The derived color space specified by x, y, and Y is known as the CIE xyY color space and is widely used to specify colors in practice.

The X and Z tristimulus values can be calculated back from the chromaticity values x and y and the Y tristimulus value:

RGB

You are certainly familiar with the RGB color space. It's the most widely used color space and, as a graphics programmer, it's the one we are dealing with everyday whether it's stored in image files or used in runtime textures. Also, 3D renderers and shaders exclusively deal with RGB values.

Despite its familiarity, it is not obvious to understand that RGB is not a device-independent format but is strongly tainted by the various stages of the color pipeline an image goes through, from acquisition to display.

Also, RGB represents a limited part of the entire color gamut which is represented by the horseshoe chromaticity diagram of the xyY color space described earlier.

It's important to understand that a RGB color is inherently tied to a Color Profile and cannot be interpreted as a standalone color.

To be perfectly accurate, a RGB color should be transformed into the master XYZ color space thanks to its color profile data which will then yield a device-independent color.

Conversely, the device-independent XYZ color can then be transformed back into RGB with maybe some other associated color profile. For example, to be stored to disk or printed.

Transformation of device-dependent colors into XYZ and back again is the role of a Color Management System, such systems are embedded in various Operating Systems but also in softwares like Adobe Photoshop.

You can find various transform operations from device-dependent color spaces to XYZ here : Color_Transforms

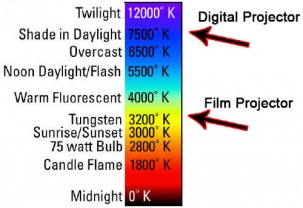
Black Body

The color (chromaticity) of blackbody radiation depends on the temperature of the black body; the locus of such colors, shown here in CIE 1931 x,y space, is known as the Planckian locus.

(source http://en.wikipedia.org/wiki/Planck%27s_law)

A black body is an idealized physical body that absorbs all incident electromagnetic radiation. Because of this perfect absorptivity at all wavelengths, a black body is also the best possible emitter of thermal radiation, which it radiates incandescently in a characteristic, continuous spectrum that depends on the body's temperature. At Earth-ambient temperatures this emission is in the infrared region of the electromagnetic spectrum and is not visible. The object appears black, since it does not reflect or emit any visible light.

The thermal radiation from a black body is energy converted electrodynamically from the body's pool of internal thermal energy at any temperature greater than absolute zero. It is called blackbody radiation and has a frequency distribution with a characteristic frequency of maximum radiative power that shifts to higher frequencies with increasing temperature. As the temperature increases past a few hundred degrees Celsius, black bodies start to emit visible wavelengths, appearing red, orange, yellow, white, and blue with increasing temperature. When an object is visually white, it is emitting a substantial fraction as ultraviolet radiation.

In terms of wavelength (λ), Planck's law is written:

<math>B_\lambda(T) =\frac{2 hc^2}{\lambda^5}\frac{1}{ e^{\frac{hc}{\lambda k_\mathrm{B}T}} - 1}</math>

where B is the spectral radiance, T is the absolute temperature of the black body, k_B is the Boltzmann constant, h is the Planck constant, and c is the speed of light.

Correlated Color Temperature (CCT)

Temperature	Source
1,700 K	Match flame
1,850 K	Candle flame, sunset/sunrise
2,700–3,300 K	Incandescent light bulb
3,200 K	Studio lamps, photofloods, etc.
3,350 K	Studio "CP" light
4,100–4,150 K	Moonlight, xenon arc lamp
5,000 K	Horizon daylight
5,500–6,000 K	Vertical daylight, electronic flash
6,500 K	Daylight, overcast
6,500–9,300 K	LCD or CRT screen
These temperatures are merely characteristic; considerable variation may be present.

CIE Illuminants

Used for :

Describing general lighting conditions (when taking a picture, or displaying one).
Spectral characteristics similar to natural light sources
Reproducible in the laboratory

The white point of an illuminant is the chromaticity of a white object under the illuminant.

1931 Illuminants

Illuminant A = Typical Incandescent Light (2856 K)
Illuminant B = Direct Sunlight
Illuminant C = Average daylight from total sky (ambient sky light)

1963 Illuminants

Illuminant D = Phases of daylight.
Necessarily followed by the first 2 digits of the CCT (e.g. D65 = D 6504K)
Represent daylight more completely and accurately than do Illuminants B and C because the spectral distributions for the D Illuminants have been defined across the ultraviolet (UV), visible, and near-infrared (IR) wavelengths (300–830 nm).
Most industries use D65 when daylight viewing conditions are required
D50 is used by graphic arts industry => more spectrally balanced across spectrum

Please refer to the D Illuminant Computation page for an interesting way of computing the SPD from CCT.

Other Illuminants

Illuminant E = Equal energy illuminant
Illuminant F = Fluorescent lamps of different composition.
- F1–F6 "standard" fluorescent lamps consist of two semi-broadband emissions of antimony and manganese activations in calcium halophosphate phosphor.
- F4 is of particular interest since it was used for calibrating the CIE Color Rendering Index (the CRI formula was chosen such that F4 would have a CRI of 51).
- F7–F9 are "broadband" (full-spectrum light) fluorescent lamps with multiple phosphors, and higher CRIs.
- F10–F12 are narrow triband illuminants consisting of three "narrowband" emissions (caused by ternary compositions of rare-earth phosphors) in the R,G,B regions of the visible spectrum. The phosphor weights can be tuned to achieve the desired CCT.

White Point

The white point is a very important data as it defines the color "white" in image capture, encoding, or reproduction. Depending on the application, different definitions of white are needed to give acceptable results. For example, photographs taken indoors may be lit by incandescent lights, which are relatively orange compared to daylight. Defining "white" as daylight will give unacceptable results when attempting to color correct a photograph taken with incandescent lighting.

Illuminant and white point are separate concepts. For a given illuminant, its white point is uniquely defined. A given white point, on the other hand, generally does not uniquely correspond to only one illuminant. From the commonly used CIE 1931 chromaticity diagram, it can be seen that almost all non-spectral colors, including colors described as white, can be produced by infinitely many combinations of spectral colors, and therefore by infinitely many different illuminant spectra.

(source from http://en.wikipedia.org/wiki/Standard_illuminant#White_point)

The spectrum of a standard illuminant, like any other profile of light, can be converted into tristimulus values. The set of three tristimulus coordinates of an illuminant is called a white point. If the profile is normalised, then the white point can equivalently be expressed as a pair of chromaticity coordinates. If an image is recorded in tristimulus coordinates (or in values which can be converted to and from them), then the white point of the illuminant used gives the maximum value of the tristimulus coordinates that will be recorded at any point in the image, in the absence of fluorescence. It is called the white point of the image. The process of calculating the white point discards a great deal of information about the profile of the illuminant, and so although it is true that for every illuminant the exact white point can be calculated, it is not the case that knowing the white point of an image alone tells you a great deal about the illuminant that was used to record it.

White points of standard illuminants

A list of standardized illuminants, their CIE chromaticity coordinates (x,y) of a perfect reflecting (or transmitting) diffuser, and their correlated color temperatures (CCTs) are given below. The CIE chromaticity coordinates are given for both the 2 degree field of view (1931) and the 10 degree field of view (1964). The color swatches represent the hue of each white point, calculated with luminance Y=0.54 and the standard observer, assuming correct sRGB display calibration.

**White points**
Name	CIE 1931 2°		CIE 1964 10°		CCT (K)	Hue	Note
Name	x₂	y₂	x₁₀	y₁₀	CCT (K)	Hue	Note
A	0.44757	0.40745	0.45117	0.40594	2856		Incandescent / Tungsten
B	0.34842	0.35161	0.34980	0.35270	4874		{obsolete} Direct sunlight at noon
C	0.31006	0.31616	0.31039	0.31905	6774		{obsolete} Average / North sky Daylight
D50	0.34567	0.35850	0.34773	0.35952	5003		Horizon Light. ICC profile PCS
D55	0.33242	0.34743	0.33411	0.34877	5503		Mid-morning / Mid-afternoon Daylight
D65	0.31271	0.32902	0.31382	0.33100	6504		Noon Daylight: Television, sRGB color space
D75	0.29902	0.31485	0.29968	0.31740	7504		North sky Daylight
E	1/3	1/3	1/3	1/3	5454		Equal energy
F1	0.31310	0.33727	0.31811	0.33559	6430		Daylight Fluorescent
F2	0.37208	0.37529	0.37925	0.36733	4230		Cool White Fluorescent
F3	0.40910	0.39430	0.41761	0.38324	3450		White Fluorescent
F4	0.44018	0.40329	0.44920	0.39074	2940		Warm White Fluorescent
F5	0.31379	0.34531	0.31975	0.34246	6350		Daylight Fluorescent
F6	0.37790	0.38835	0.38660	0.37847	4150		Lite White Fluorescent
F7	0.31292	0.32933	0.31569	0.32960	6500		D65 simulator, Daylight simulator
F8	0.34588	0.35875	0.34902	0.35939	5000		D50 simulator, Sylvania F40 Design 50
F9	0.37417	0.37281	0.37829	0.37045	4150		Cool White Deluxe Fluorescent
F10	0.34609	0.35986	0.35090	0.35444	5000		Philips TL85, Ultralume 50
F11	0.38052	0.37713	0.38541	0.37123	4000		Philips TL84, Ultralume 40
F12	0.43695	0.40441	0.44256	0.39717	3000		Philips TL83, Ultralume 30

References

An Introduction to Appearance Analysis (2001) http://www.color.org/ss84.pdf

Colorimetry

Views

Contents