| Line 13: | Line 13: | ||
And '''that is all''' there is to it! Now let's see how to execute the 2 parts of the algorithm. | And '''that is all''' there is to it! Now let's see how to execute the 2 parts of the algorithm. | ||
| − | ==Part 1: Transforming any sequence of numbers into a bitonic sequence== | + | ==Quick Algorithm== |
| + | ===Part 1: Transforming any sequence of numbers into a bitonic sequence=== | ||
It's a log2(N) algorithm where we recursively compare and swap elements 2 by 2 in a very specific manner. | It's a log2(N) algorithm where we recursively compare and swap elements 2 by 2 in a very specific manner. | ||
| Line 25: | Line 26: | ||
[[File:BitonicBuild1.png]] | [[File:BitonicBuild1.png]] | ||
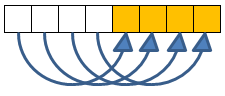
| + | Finally we perform 4 compares&swaps like this: | ||
| + | [[File:BitonicBuild2.png]] | ||
| − | ==Part 2: Sorting the bitonic sequence== | + | |
| + | ===Part 2: Sorting the bitonic sequence=== | ||
Well it's another log2(N) algorithm as in part 1. You'll need to swap numbers log2(N) times. | Well it's another log2(N) algorithm as in part 1. You'll need to swap numbers log2(N) times. | ||
| Line 42: | Line 46: | ||
[[File:BitonicCompare2.png]] | [[File:BitonicCompare2.png]] | ||
| + | |||
| + | |||
| + | ==The way I see it== | ||
| + | |||
| + | |||
| + | ==Example== | ||
Revision as of 15:05, 11 September 2015
I wanted to write a short explanation about bitonic sort because it's simple as hell but no one does a good job at explaining it correctly.
You can find the video explanation here https://www.youtube.com/watch?v=GEQ8y26blEY but it's a bit tedious so to sum up the algorithm, here's what you need to know:
- A bitonic sequence is a sequence of numbers that can be ordered as first ascending then descending (or the opposite)
- For example: (1, 2, 3, 4) followed by (4,3,2,1) is bitonic.
- The bitonic sort algorithm works in 2 parts:
- (1) First, you need to transform any random sequence of numbers into a bitonic sequence
- (2) Second, you can then sort the bitonic sequence in ascending order
And that is all there is to it! Now let's see how to execute the 2 parts of the algorithm.
Contents
Quick Algorithm
Part 1: Transforming any sequence of numbers into a bitonic sequence
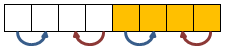
It's a log2(N) algorithm where we recursively compare and swap elements 2 by 2 in a very specific manner.
For 8 values, we first perform 4 compare&swaps like this:
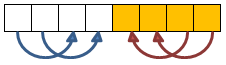
Then we perform 4 compares&swaps like this:
Finally we perform 4 compares&swaps like this:
Part 2: Sorting the bitonic sequence
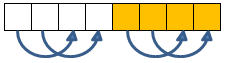
Well it's another log2(N) algorithm as in part 1. You'll need to swap numbers log2(N) times.
For 8 values, we first perform 4 compares&swaps like this:
Then we perform 4 compares&swaps like this:
Finally we perform 4 compares&swaps like this: