| Line 2: | Line 2: | ||
[[File:NylonBRDF.jpg|thumb|right|600px|The BRDF of nylon viewed in the [http://www.disneyanimation.com/technology/brdf.html Disney BRDF Explorer]. The cyan line represents the incoming light direction, the red peanut object is the amount of light reflected in the corresponding direction.]] | [[File:NylonBRDF.jpg|thumb|right|600px|The BRDF of nylon viewed in the [http://www.disneyanimation.com/technology/brdf.html Disney BRDF Explorer]. The cyan line represents the incoming light direction, the red peanut object is the amount of light reflected in the corresponding direction.]] | ||
| − | |||
===So, what's a BRDF?=== | ===So, what's a BRDF?=== | ||
As I see it, it's an abstract tool that helps us to describe the macroscopic behavior of materials when photons hit this material. It's a convenient black box, a huge multi-dimensional lookup table (3, 4, or sometimes 5, 6 dimensions when including space variations) that somehow encodes the amount of photons bouncing off the surface in a specific (outgoing) direction when coming from another specific (incoming) direction (and potentially, from another location). | As I see it, it's an abstract tool that helps us to describe the macroscopic behavior of materials when photons hit this material. It's a convenient black box, a huge multi-dimensional lookup table (3, 4, or sometimes 5, 6 dimensions when including space variations) that somehow encodes the amount of photons bouncing off the surface in a specific (outgoing) direction when coming from another specific (incoming) direction (and potentially, from another location). | ||
| + | |||
===It comes in many flavours=== | ===It comes in many flavours=== | ||
| Line 17: | Line 17: | ||
* The BSSRDF (Surface Scattering Reflectance) is a much larger model that also accounts for different locations for the incoming and outgoing rays. It thus becomes 5- or even 6-dimensional. | * The BSSRDF (Surface Scattering Reflectance) is a much larger model that also accounts for different locations for the incoming and outgoing rays. It thus becomes 5- or even 6-dimensional. | ||
| − | |||
| − | |||
===First, what's the color of a pixel?=== | ===First, what's the color of a pixel?=== | ||
| Line 25: | Line 23: | ||
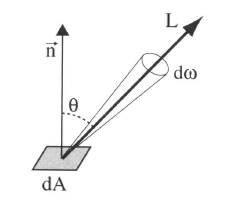
Radiance is the radiant flux of photons per unit area per unit solid angle and is written as <math>L(x,\omega)</math>. Its unit is the Watt per square meter per steradian (<math>W.m^{-2}.sr^{-1}</math>). | Radiance is the radiant flux of photons per unit area per unit solid angle and is written as <math>L(x,\omega)</math>. Its unit is the Watt per square meter per steradian (<math>W.m^{-2}.sr^{-1}</math>). | ||
* <math>x</math> is the location where the radiance is evaluated, it's a ''3D vector''! | * <math>x</math> is the location where the radiance is evaluated, it's a ''3D vector''! | ||
| − | * <math>\omega</math> is the direction in which the radiance is evaluated, it's also a ''3D vector'' but it's normalized so it can be written as <math>\langle \ | + | * <math>\omega</math> is the direction in which the radiance is evaluated, it's also a ''3D vector'' but it's normalized so it can be written as <math>\langle \phi,\theta \rangle</math> couple of spherical coordinates. |
| − | The radiant flux of photons –or simply ''flux''– is basically the amount of photons | + | The radiant flux of photons –or simply ''flux''– is basically the amount of photons/energy per amount of time. |
| + | And since we're considering a single CCD sensor element or a single photo-receptor in the back of the eye: | ||
* We only perceive that flux in a single location, hence the "per square meter". We take the flux flowing through an infinitesimal piece of surface. | * We only perceive that flux in a single location, hence the "per square meter". We take the flux flowing through an infinitesimal piece of surface. | ||
* We only perceive that flux in a single direction, hence the "per steradian". We take the flux flowing through an infinitesimal piece of the whole sphere of directions (a.k.a. a ray!) | * We only perceive that flux in a single direction, hence the "per steradian". We take the flux flowing through an infinitesimal piece of the whole sphere of directions (a.k.a. a ray!) | ||
| Line 43: | Line 42: | ||
And guess what's this special function? | And guess what's this special function? | ||
| + | Well, yes! It's the BRDF and it's used to completely describe the behavior of radiance when it interacts with a material. Any material... | ||
| − | == | + | |
| − | + | == Mathematically == | |
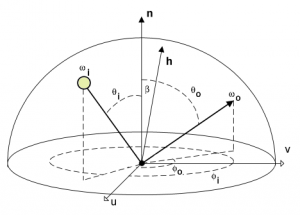
We're going to use <math>\omega_i</math> and <math>\omega_o</math> to denote the incoming and outgoing directions respectively. Each of these 2 directions are encoded in spherical coordinates by a couple of angles <math>\langle \phi_i,\theta_i \rangle</math> and <math>\langle \phi_o,\theta_o \rangle</math>. | We're going to use <math>\omega_i</math> and <math>\omega_o</math> to denote the incoming and outgoing directions respectively. Each of these 2 directions are encoded in spherical coordinates by a couple of angles <math>\langle \phi_i,\theta_i \rangle</math> and <math>\langle \phi_o,\theta_o \rangle</math>. | ||
Revision as of 21:45, 25 December 2012
Contents
[hide]Characteristics of a BRDF

So, what's a BRDF?
As I see it, it's an abstract tool that helps us to describe the macroscopic behavior of materials when photons hit this material. It's a convenient black box, a huge multi-dimensional lookup table (3, 4, or sometimes 5, 6 dimensions when including space variations) that somehow encodes the amount of photons bouncing off the surface in a specific (outgoing) direction when coming from another specific (incoming) direction (and potentially, from another location).
It comes in many flavours
A Bidrectional Reflectance Distribution Function or BRDF is only a subset of the phenomena that happen when photons hit a material but there are plenty of other kinds of BxDFs:
- The BRDF only deals about reflection, so we're talking about photons come from outside the material and scatter back outside the material as well.
- The BTDF (Transmittance) only deals about transmission of photons coming from outside the material and scattering inside the material (i.e. refraction).
- Note that the BRDF and BTDF only need to consider the upper or lower hemispheres of directions (which we call <math>\Omega</math>, or sometimes <math>\Omega_+</math> and <math>\Omega_-</math> if the distinction is required)
- The BSDF (Scattering) is the general term that encompasses both the BRDF and BTDF. This time, it considers the entire sphere of directions.
- Anyway, the BSDF, BRDF and BTDF iares generally 4-dimensional as they make the (usually correct) assumption that both the incoming and outgoing rays interact with the material at a unique and same location.
- Also, the BSDF could be viewed as an incorrect term since it also accounts for the other phenomenon happening to photons when they hit a material: absorption.
- The BSSRDF (Surface Scattering Reflectance) is a much larger model that also accounts for different locations for the incoming and outgoing rays. It thus becomes 5- or even 6-dimensional.
First, what's the color of a pixel?
Well, a pixel encodes what the eye or a CCD sensor is sensitive to: it's called radiance.
Radiance is the radiant flux of photons per unit area per unit solid angle and is written as <math>L(x,\omega)</math>. Its unit is the Watt per square meter per steradian (<math>W.m^{-2}.sr^{-1}</math>).
- <math>x</math> is the location where the radiance is evaluated, it's a 3D vector!
- <math>\omega</math> is the direction in which the radiance is evaluated, it's also a 3D vector but it's normalized so it can be written as <math>\langle \phi,\theta \rangle</math> couple of spherical coordinates.
The radiant flux of photons –or simply flux– is basically the amount of photons/energy per amount of time.
And since we're considering a single CCD sensor element or a single photo-receptor in the back of the eye:
- We only perceive that flux in a single location, hence the "per square meter". We take the flux flowing through an infinitesimal piece of surface.
- We only perceive that flux in a single direction, hence the "per steradian". We take the flux flowing through an infinitesimal piece of the whole sphere of directions (a.k.a. a ray!)
So the radiance is this: the amount of photons per seconds flowing along a ray and reaching a single location. And that's what is stored in the pixels of an image.
A good example is a cube map used for Image Based Lighting (IBL): each texel of the cube map represents a piece of the photon flux reaching the point at the center of the cube map. It encodes the entire light field around an object and if you use the cube map well, your object can seamlessly integrate into the real environment where the cube map photograph was taken (thanks to our dear Paul Debevec) (ever noticed how movies before 1999 had poor CGI? And since his paper on HDR probes, it's a real orgy! ![]() ).
).
But IBL is also very expensive: ideally, you would need to integrate each texel of the cube map and dot it with your normal and multiply it by some special function to obtain the perceived color of your surface in the view direction.
And guess what's this special function?
Well, yes! It's the BRDF and it's used to completely describe the behavior of radiance when it interacts with a material. Any material...
Mathematically
We're going to use <math>\omega_i</math> and <math>\omega_o</math> to denote the incoming and outgoing directions respectively. Each of these 2 directions are encoded in spherical coordinates by a couple of angles <math>\langle \phi_i,\theta_i \rangle</math> and <math>\langle \phi_o,\theta_o \rangle</math>. These only represent generic directions, we don't care if it's a view direction or light direction.
For example, for radiance estimates, the outgoing direction is usually the view direction while the incoming direction is the light direction. For importance estimates, it's the opposite.
Also note that we use vectors pointing toward the view or the light.
Integration of radiance arriving at a point on a surface, times <math>n.\omega_i</math> yields the irradiance (<math>W.m^{-2}</math>):
<math> E_r(x) = \int_\Omega dE_i(x,\omega_i) = \int_\Omega L_i(x,\omega_i) (n.\omega_i) \, d\omega_i </math>
But when we inject the BRDF into the integral, we obtain a new radiance :
<math>L_r(x,\omega_o) = \int_\Omega f_r(x,\omega_o,\omega_i) L_i(\omega_i) (n.\omega_i) \, d\omega_i</math>
Indeed, the expression of the BRDF (<math>sr^{-1}</math>) is:
<math>f_r(x,\omega_o,\omega_i) = \frac{dL_r(x,\omega_o)}{dE_i(x,\omega_i)}</math>
From the first equation of the irradiance, we can deduce that:
<math>dE_i(x,\omega_i) = L_i(x,\omega_i) (n.\omega_i) d\omega_i</math> (note that we simply removed the integral signs to get this)
We can then rewrite the BRDF as:
<math>f_r(x,\omega_o,\omega_i) = \frac{dL_r(x,\omega_o)}{L_i(x,\omega_i) (n.\omega_i) d\omega_i}</math>
It can be seen as the infinitesimal amount of reflected radiance by the infinitesimal amount of incoming irradiance.
We thus realize it's defined as an infinitesimal quantity (so we need to integrate it to obtain the final result) and it's expressed in <math>sr^{-1}</math> units.
The fundamental characteristics of a real material BRDf are:
- Reciprocity (a.k.a. Helmoltz principle), guaranteeing the BRDF returns the same value if <math>\omega_o</math> and <math>\omega_i</math> are reversed (i.e. view is swapped with light).
- Energy conservation, guaranteeing the total amount of reflected light is less or equal to the amount of incoming light.
Sources
I've been reading interesting papers from the Siggraph 2012 talk about Practical Physically Based Shading in Film and Game Production which is available here
Some ideas and generalizations/ideas/explanations are worth mentioning.
From "Background: Physics and Math of Shading (Naty Hoffman)" I learned that:
- metals completely absorb photons if they are not reflected specularly: metals have no diffuse components.
- Moreover, metals usually have a colored specular (due to RGB variations in the Fresnel reflections) while dielectric materials have a uniform specular and need only luminance encoding.