| Line 10: | Line 10: | ||
In terms of wavelength (''λ''), Planck's law is written: | In terms of wavelength (''λ''), Planck's law is written: | ||
| − | <math>B_\lambda(T) =\frac{2 hc^2}{\lambda^5}\frac{1}{ e^{\frac{hc}{\lambda k_\mathrm{B}T}} - 1}</math> | + | :<math>B_\lambda(T) =\frac{2 hc^2}{\lambda^5}\frac{1}{ e^{\frac{hc}{\lambda k_\mathrm{B}T}} - 1}</math> |
where ''B'' is the spectral radiance, ''T'' is the absolute temperature of the black body, ''k''<sub>B</sub> is the Boltzmann constant, ''h'' is the Planck constant, and ''c'' is the speed of light. However these are not the only ways to express the law; expressing it in terms of wavenumber rather than frequency or wavelength is also common, as are expression in terms of the number of photons emitted at a certain wavelength, rather than energy emitted. In the limit of low frequencies (i.e. long wavelengths), Planck's law becomes the Rayleigh–Jeans law, while in the limit of high frequencies (i.e. small wavelengths) it tends to the Wien approximation. | where ''B'' is the spectral radiance, ''T'' is the absolute temperature of the black body, ''k''<sub>B</sub> is the Boltzmann constant, ''h'' is the Planck constant, and ''c'' is the speed of light. However these are not the only ways to express the law; expressing it in terms of wavenumber rather than frequency or wavelength is also common, as are expression in terms of the number of photons emitted at a certain wavelength, rather than energy emitted. In the limit of low frequencies (i.e. long wavelengths), Planck's law becomes the Rayleigh–Jeans law, while in the limit of high frequencies (i.e. small wavelengths) it tends to the Wien approximation. | ||
Revision as of 17:46, 29 December 2011
Black Body
A black body is an idealized physical body that absorbs all incident electromagnetic radiation. Because of this perfect absorptivity at all wavelengths, a black body is also the best possible emitter of thermal radiation, which it radiates incandescently in a characteristic, continuous spectrum that depends on the body's temperature. At Earth-ambient temperatures this emission is in the infrared region of the electromagnetic spectrum and is not visible. The object appears black, since it does not reflect or emit any visible light.
The thermal radiation from a black body is energy converted electrodynamically from the body's pool of internal thermal energy at any temperature greater than absolute zero. It is called blackbody radiation and has a frequency distribution with a characteristic frequency of maximum radiative power that shifts to higher frequencies with increasing temperature. As the temperature increases past a few hundred degrees Celsius, black bodies start to emit visible wavelengths, appearing red, orange, yellow, white, and blue with increasing temperature. When an object is visually white, it is emitting a substantial fraction as ultraviolet radiation.
In terms of wavelength (λ), Planck's law is written:
- <math>B_\lambda(T) =\frac{2 hc^2}{\lambda^5}\frac{1}{ e^{\frac{hc}{\lambda k_\mathrm{B}T}} - 1}</math>
where B is the spectral radiance, T is the absolute temperature of the black body, kB is the Boltzmann constant, h is the Planck constant, and c is the speed of light. However these are not the only ways to express the law; expressing it in terms of wavenumber rather than frequency or wavelength is also common, as are expression in terms of the number of photons emitted at a certain wavelength, rather than energy emitted. In the limit of low frequencies (i.e. long wavelengths), Planck's law becomes the Rayleigh–Jeans law, while in the limit of high frequencies (i.e. small wavelengths) it tends to the Wien approximation.
(source http://en.wikipedia.org/wiki/Planck%27s_law)
RUFF STUFF
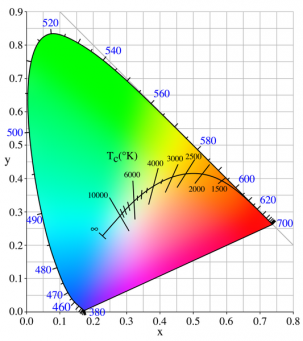
CCT = Correlated Color Temperature (6500K, etc.)
CIE Illuminants =>
- General lighting conditions (when taking a picture, or displaying one).
- Spectral characteristics similar to natural light sources
- Reproducible in the laboratory
1931 Illuminants:
- Illuminant A = Typical Incandescent Light (2856 K)
- Illuminant B = Direct Sunlight
- Illuminant C = Average daylight from total sky (ambient sky light)
1963 D Illuminants (more accurate daylight conditions):
- Illuminant D = Phases of daylight. Necessarily followed by the first 2 digits of the CCT (e.g. D65 = D 6504K)
- Represent daylight more completely and accurately than do Illuminants B and C because the spectral distributions for the D Illuminants have been defined across the ultraviolet (UV), visible, and near-infrared (IR) wavelengths (300–830 nm).
- Most industries use D65 when daylight viewing conditions are required
- D50 is used by graphic arts industry => more spectrally balanced across spectrum
Other illuminants:
- Illuminant E = Equal energy illuminant
- Illuminant F = Fluorescent lamps of different composition.
References
An Introduction to Appearance Analysis (2001) http://www.color.org/ss84.pdf