| Line 11: | Line 11: | ||
| − | + | ==Cubemap Projection Configuration== | |
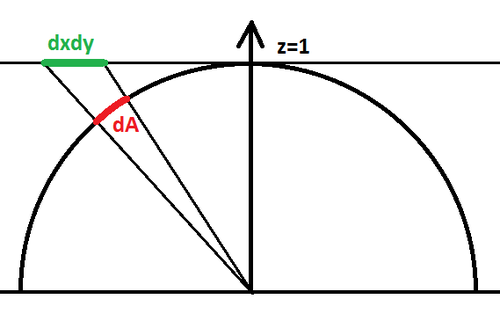
| − | The configuration for a cube map is | + | The configuration for a cube map is that pixels are lying on a plane z=1 such as <math>p'=(x,y,1), -1<x<1, -1<y<1</math> and we project back onto the unit hemisphere by "normalizing" the vector <math>p=\frac{p'}{|p'|}=\frac{(x,y,1)}{\sqrt{1+x^2+y^2}}</math> as shown on the figure below: |
| + | [[File:PerspectiveProjection.png|500px]] | ||
| − | + | ||
| + | |||
| + | ==Our Projection Configuration== | ||
Revision as of 17:44, 2 June 2017
Hi!
Maybe you already bumped into the problem of projecting a cubemap into spherical harmonics and found this page to help you out: http://www.rorydriscoll.com/2012/01/15/cubemap-texel-solid-angle/ ?
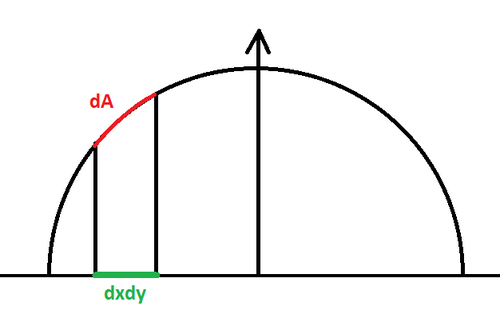
But maybe you need the solution of another, similar problem that consists in finding the solid angle of a pixel lying in the z=0 plane and orthogonally projected onto the hemisphere, like shown here:
First of all, the document that was used initially to do the computations, both in AMD's cube map generator, Rory Driscoll's summary and this page, is the very interesting thesis by Manne Öhrström.
Cubemap Projection Configuration
The configuration for a cube map is that pixels are lying on a plane z=1 such as <math>p'=(x,y,1), -1<x<1, -1<y<1</math> and we project back onto the unit hemisphere by "normalizing" the vector <math>p=\frac{p'}{|p'|}=\frac{(x,y,1)}{\sqrt{1+x^2+y^2}}</math> as shown on the figure below: