| (12 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | Je vais tenter de me ré-initier à une catégorie des mathématiques que mes profs de math-sup m'avaient fait détester: l' | + | Je vais tenter de me ré-initier à une catégorie des mathématiques que mes profs de math-sup m'avaient fait détester: l'algèbre. Et plus particulièrement, la théorie des groupes. |
Comme c'est souvent le cas avec les sujets qu'on me force à ingurgiter, je mets un points d'honneur à n'en rien retenir. Je vais donc tout reprendre de zéro... Ces pages me serviront de notes de lecture et suivront l'ordre dans lequel je me serai de nouveau familiarisé avec ce sujet. | Comme c'est souvent le cas avec les sujets qu'on me force à ingurgiter, je mets un points d'honneur à n'en rien retenir. Je vais donc tout reprendre de zéro... Ces pages me serviront de notes de lecture et suivront l'ordre dans lequel je me serai de nouveau familiarisé avec ce sujet. | ||
| Line 32: | Line 32: | ||
La démonstration, bien que nécessaire à la classification de la proposition comme « théorème », n'est pas considérée comme faisant partie du théorème. | La démonstration, bien que nécessaire à la classification de la proposition comme « théorème », n'est pas considérée comme faisant partie du théorème. | ||
| − | |||
La démonstration comprend : | La démonstration comprend : | ||
* des axiomes ; | * des axiomes ; | ||
| Line 39: | Line 38: | ||
Chaque étape de la preuve est liée aux précédentes par des règles d'inférence logiques. | Chaque étape de la preuve est liée aux précédentes par des règles d'inférence logiques. | ||
| + | |||
| + | ====D'autres formes d'assertions==== | ||
| + | Au sens large toute assertion effectivement démontrée peut prendre le nom de théorème. Dans les ouvrages de mathématiques, il est cependant d'usage de réserver ce terme aux affirmations considérées comme nouvelles ou particulièrement intéressantes ou importantes. Selon leur importance, ou leur utilité, les autres assertions peuvent prendre des noms différents : | ||
| + | * '''lemme''' : assertion servant d'intermédiaire pour démontrer un théorème plus important ; | ||
| + | * '''corollaire''' : résultat qui découle directement d’un théorème prouvé ; on trouve aussi, dans les ouvrages anciens, le terme scholie. (Voir wikt:corollaire) | ||
| + | * '''proposition''' : résultat relativement simple qui n'est pas associé avec un théorème particulier ; | ||
| + | * '''remarque''' : résultat intéressant ou conséquence qui peut faire partie de la preuve ou d'une autre affirmation ; | ||
| + | * '''conjecture''' : proposition mathématique dont on ignore la valeur de vérité. Une fois prouvée, une conjecture devient un théorème. | ||
| Line 46: | Line 53: | ||
Un '''ensemble''' désigne intuitivement une collection d’objets (les éléments de l'ensemble), « une multitude qui peut être comprise comme un tout » (au sens d'omnis). | Un '''ensemble''' désigne intuitivement une collection d’objets (les éléments de l'ensemble), « une multitude qui peut être comprise comme un tout » (au sens d'omnis). | ||
| + | Dans une approche axiomatique, la théorie des ensembles est une théorie de l'appartenance (un élément d'un ensemble est dit « appartenir » à cet ensemble). Le mot ensemble désigne alors un objet du domaine de cette théorie, dont les axiomes régissent les propriétés. La théorie des ensembles est utilisée pour fonder les mathématiques, et dans cette approche tout objet mathématique est in fine un ensemble. | ||
| + | |||
| + | La formulation en reviendrait au mathématicien [http://fr.wikipedia.org/wiki/Georg_Cantor Georg Cantor], qui énonçait : « Par ensemble, nous entendons toute collection M d'objets m de notre intuition ou de notre pensée, définis et distincts, ces objets étant appelés les éléments de M » | ||
| + | |||
| + | Les éléments peuvent être de n’importe quelle nature : nombres, points géométriques, droites, fonctions, autres ensembles... | ||
| + | |||
| + | L'appartenance d'un élément, noté par exemple x, à un ensemble, noté par exemple A, s’écrit : x ∈ A. | ||
| + | |||
| + | |||
| + | On dira donc que deux ensembles A et B sont égaux (on le notera comme d'habitude A = B) quand ils ont exactement les mêmes éléments. Cette propriété est connue sous le nom d'extensionnalité : | ||
| + | |||
| + | A = B si et seulement si ∀x (x ∈ A ⇔ x ∈ B) | ||
| + | où « ⇔ » désigne l'équivalence logique. | ||
| + | |||
| + | ====Exemples==== | ||
| + | * L'ensemble auxquels appartiennent les éléments 2, 3, et 5, et seulement ces éléments, est noté {2, 3, 5}. L'ensemble est défini en ''extension''. | ||
| + | * La façon la plus générale de définir un ensemble est de donner une propriété caractéristique des éléments de cet ensemble. Par exemple, on pourra définir l'ensemble des nombres premiers par une propriété caractéristique de ceux-ci : être différent de 1 et avoir pour seuls diviseurs 1 et lui-même. On parle de définition en ''compréhension''. | ||
| + | * Par extensionnalité, il n'y a qu'un seul ensemble sans éléments, l'ensemble vide, que l'on note ∅ ou { }. | ||
| + | * L'ensemble des entiers naturels pairs : <math>\{x \in\mathbb{N}\mid x\ \rm pair \}</math>. | ||
| + | * On définira de la même façon (ℤ désignant l'ensemble des entiers relatifs) : | ||
| + | ** <math>\{x \in\mathbb{Z}\mid -7 \leq x \leq 23\}</math> l'ensemble des entiers relatifs compris entre -7 et 23 ; | ||
| + | ** <math>\left\{x \in\mathbb{N}\mid \exists y \in \mathbb{N}\ (y \geq 1\ {\rm et}\ x = y^2)\right\}</math> l'ensemble des carrés parfaits non nuls. | ||
| + | |||
| + | |||
| + | ===Intervalle=== | ||
| + | En mathématiques, un '''intervalle''' (du latin intervallum) est étymologiquement un ensemble compris entre deux valeurs. Cette notion première s'est ensuite développée jusqu'à aboutir aux définitions suivantes. | ||
| + | |||
| + | |||
| + | Initialement, on appelle intervalle réel un ensemble de nombres délimité par deux nombres réels constituant une borne inférieure et une borne supérieure. Un intervalle contient tous les nombres réels compris entre ces deux bornes. | ||
| + | |||
| + | Cette définition regroupe les intervalles des types suivants (avec <math>(a,b)\in\mathbb{R}^2,\ a<b</math>): | ||
| + | |||
| + | * <math>\{x\in\mathbb{R} \mid a < x < b \} = \;]a; b[</math> (ouvert et non fermé) | ||
| + | * <math>\{x\in\mathbb{R} \mid a \leq x \leq b \} = [a ; b]</math> (fermé et non ouvert) | ||
| + | * <math>\{x\in\mathbb{R} \mid a < x \leq b \} = \;]a; b]</math> (ni ouvert, ni fermé) | ||
| + | * <math>\{x\in\mathbb{R} \mid a \leq x < b \} = [a; b[</math> (ni ouvert, ni fermé) | ||
| + | |||
| + | Les intervalles du premier type sont appelés intervalles ouverts ; les seconds intervalles fermés, et les deux derniers intervalles semi-ouverts. | ||
| + | |||
| + | ====Union et intersection==== | ||
| + | * Une intersection d'intervalles de <math>\mathbb{R}</math> est toujours un intervalle. | ||
| + | * Une union d'intervalles de <math>\mathbb{R}</math> n'est pas toujours un intervalle. Ce sera un intervalle si l'ensemble obtenu reste convexe (intuitivement s'il n'y a pas de "trou"). Dans le cas d'une union de deux intervalles, il suffit que l'intersection de ces intervalles soit non vide pour que leur réunion soit convexe. | ||
| + | |||
| + | ====En [http://fr.wikipedia.org/wiki/Analyse_(math%C3%A9matiques) analyse] et en topologie==== | ||
| + | Les intervalles sont les parties de <math>\mathbb{R}</math> les plus intéressantes dès que l'on parle de continuité et de dérivabilité. | ||
| + | |||
| + | On trouve alors (entre autres) pour les fonctions réelles d'une variable réelle, des propriétés telles que : | ||
| + | * L'image par une fonction continue d'un intervalle de <math>\mathbb{R}</math> est un intervalle de <math>\mathbb{R}</math> (théorème des valeurs intermédiaires) | ||
| + | * Une fonction dérivable et à dérivée identiquement nulle sur un intervalle est constante sur cet intervalle. | ||
| + | * Une fonction dérivable est monotone sur un intervalle si et seulement si sa dérivée garde un signe constant sur cet intervalle | ||
| + | |||
| + | |||
| + | ===Loi de Composition Interne=== | ||
| + | Une '''loi de composition interne''' (ou, parfois, opération) est un procédé qui, à deux éléments d'un ensemble E, associe un troisième élément de E. L'addition et la multiplication sont des exemples classiques de lois de composition interne des ensembles de nombres usuels, tels que les entiers naturels. | ||
| + | |||
| + | Nous avons tous depuis le primaire une assez bonne idée de la notion d'opérations telles que l'addition, la soustraction, la multiplication ou la division. Une '''opération (interne)''' dans un ensemble est une relation interne dans cet ensemble, qui, à deux éléments quelconques de cet ensemble, appelés '''opérandes''', en associe éventuellement un troisième, unique, nommé '''résultat''', toujours dans ce même ensemble. | ||
| + | |||
| + | Pour que l’opération considérée soit effectivement une loi de composition interne, il faut qu’elle ait un sens quels que soient les deux éléments de l’ensemble choisis (on dit formellement que l'opération doit être définie partout). Ainsi : | ||
| + | * la division n’est pas une loi de composition interne dans <math>\mathbb{R} \,,</math> parce qu’on ne peut pas diviser par zéro : par exemple, « 3 / 0 » n’a pas de sens. Mais cette même division est une loi de composition interne dans <math>\mathbb{R}^{*} \,</math> (ensemble des réels privés de 0). Enfin cette même opération n'est pas une loi de composition interne dans <math>\mathbb{Z}^{*} \,</math> car 2 / 3 n'est pas un entier relatif. | ||
| + | * la soustraction peut être ou non une loi de composition interne selon l’ensemble de nombres considéré : | ||
| + | ** s’il s’agit de l’ensemble des nombres usuels, dits entiers naturels { 0, 1, 2, 3,... }, ce n’en est pas une, puisque « 3 - 5 », par exemple, n’a pas pour résultat l’un de ces nombres usuels. | ||
| + | ** si au contraire, on choisit l’ensemble des entiers relatifs, qui en plus des entiers naturels, contient les entiers négatifs { ..., -3, -2, -1}, alors la soustraction est bien une loi de composition interne. | ||
| + | |||
| + | En résumé, une '''loi de composition interne''' dans un ensemble E, ou, plus simplement une '''loi''' dans E, est une opération qui donne un résultat dans E pour tous les couples possibles d'éléments de E. | ||
| + | |||
| + | ====Exemple==== | ||
| + | Dans l’ensemble des entiers relatifs, l’addition est une ''loi de composition interne'' ayant entre autres les propriétés suivantes, qui seront définies plus formellement dans la seconde partie de l’article : | ||
| + | * 0 est élément '''neutre''' pour cette loi : l’ajouter à n’importe quel nombre redonne ce nombre : par exemple, 5 + 0 = 5 , et 0 + 8 = 8 ; | ||
| + | * pour tout entier, il existe un autre nombre, son '''opposé''' (le terme général est ''élément symétrique''), tel qu’ajouté au premier, il redonne l’élément neutre 0. L’''opposé'' se note comme l’entier initial changé de signe. Ainsi : 3 + (-3) = 0 ; | ||
| + | * on peut échanger les deux éléments autour du signe « <math>+</math> » : 3 + 5 = 5 + 3 = 8 . On dit que l’opération est '''commutative''' ; | ||
| + | * on peut grouper les éléments comme on le souhaite quand on en ajoute plus de deux : 3 + 5 + 4 peut se calculer de deux manières : | ||
| + | ** en calculant d’abord 3 + 5 = 8 puis en ajoutant 4 au résultat, | ||
| + | ** ou en calculant 5 + 4 = 9 avant de calculer 3 + 9 . | ||
| + | :Ces deux méthodes mènent au même résultat, ce que l’on note : (3 + 5) + 4 = 3 + (5 + 4) . On dit que l’opération est '''associative'''. | ||
| + | |||
| + | Ces quatre propriétés, ''existence d’un élément neutre'', ''existence de symétriques'', ''commutativité'', ''associativité'', peuvent se retrouver pour d’autres ensembles et d’autres lois. Ainsi, on peut étudier l’ensemble des ''translations'' (c’est-à-dire les déplacements en ligne droite : par exemple, se déplacer de 3 mètres vers la gauche et de 2 mètres vers le haut), et une loi de composition interne sur cet ensemble, la ''composition'' : la composition de deux translations consistant simplement à faire le premier déplacement, puis le second. On retrouve pour la composition les mêmes propriétés que pour l’addition : | ||
| + | * le ''neutre'' est la translation nulle, consistant à ne pas se déplacer ; | ||
| + | * le ''symétrique'' d’une translation consiste à faire le même déplacement dans l’autre sens (3 mètres à droite et 2 mètres vers le bas pour l’exemple précédent) : si on fait successivement les deux, c’est comme si on faisait le déplacement nul ; | ||
| + | * on peut faire les déplacements dans l’ordre qu’on veut, on retrouve la ''commutativité'' et l’''associativité''. | ||
| + | |||
| + | |||
| + | === Suite réelle ou complexe de Cauchy === | ||
| + | |||
| + | Une suite de réels ou de complexes <math>(r_n) \ </math> est dite '''de Cauchy''', ou vérifie le '''critère de Cauchy''', lorsque les termes de la suite se rapprochent uniformément les uns des autres en l'infini au sens où : | ||
| + | <center><math>\lim_{n\rightarrow \infty}\sup_{p,q>n}|r_p-r_q|=0</math>.</center> | ||
| + | Cette dernière condition se réécrit classiquement à l'aide de [[quantificateur (logique)|quantificateurs universels et existentiels]] : | ||
| + | <center><math>\forall\varepsilon>0,\; \exists N\in\N,\; \forall p,q>N,\; |r_p-r_q|<\varepsilon\; </math>,</center> | ||
| + | <center>ou encore : <math>\forall\varepsilon>0,\; \exists N\in\N,\; \forall n>N,\; \forall k>0,\; |r_{n+k}-r_n|<\varepsilon\;</math>.</center> | ||
| + | L'uniformité dans la définition est importante. En effet, la différence des termes consécutifs de la suite <math>(\ln(n)) \ </math> tend vers 0, et, plus précisément : | ||
| + | <center><math>\ln(n+1)-\ln(n)=\ln\left(1+\frac{1}{n}\right)=\frac{1}{n}+O\left(\frac{1}{n^2}\right)</math>.</center> | ||
| + | Cependant, <math>\ln(2n)-\ln(n)=\ln(2) \ </math> ne converge pas vers 0 lorsque ''n'' tend vers l'infini. La suite n'est donc pas de Cauchy. | ||
| + | '''Critère de Cauchy''' : Une suite <math>(r_n) \ </math> de nombres réels (respectivement complexes) converge dans ℝ (respectivement ℂ) si et seulement si c'est une suite de Cauchy. | ||
| + | ==== Suite de Cauchy dans un espace métrique ==== | ||
| + | Une [[suite (mathématiques)|suite]] <math>(x_n)_{n\in\N}</math> dans un [[espace métrique]] <math>(E,d)</math> est dite '''suite de Cauchy''' (ou '''de Cauchy''') si pour tout réel <math>\varepsilon>0</math>, il existe un [[entier naturel]] <math>N</math> tel que pour tous entiers <math>p,q\geq N</math>, la distance <math>d(x_p,x_q)</math> soit inférieure à <math>\varepsilon</math> : | ||
| + | <center><math>\forall \varepsilon>0,\; \exists N\in\N,\; \forall p,q\ge N,\; d(x_p,x_q)<\varepsilon</math></center> | ||
| + | ou plus synthétiquement, si | ||
| + | <center><math>\lim_{n\rightarrow \infty}\sup_{p,q\ge n}d(x_p,x_q)=0</math></center> | ||
| + | ou encore : | ||
| + | <center><math>\lim_{n\rightarrow \infty}\sup_{m\ge n}d(x_m,x_n)=0.</math></center> | ||
| + | Les inégalités autres que <math>\varepsilon>0</math> peuvent être prises indifféremment larges ou strictes. Lorsque certains ouvrages introduisent la notion de suite de Cauchy uniquement pour les suites de réels, c'est exactement la même définition. La distance ''d'' est simplement à remplacer par la valeur absolue de la différence. | ||
| − | == | + | Intuitivement, les termes de la suite deviennent de plus en plus proches les uns des autres d'une certaine façon qui suggère que la suite doit avoir une [[limite de suite|limite]] dans l'espace. Les suites convergentes sont effectivement de Cauchy, mais néanmoins la réciproque n'est pas vraie en toute généralité. Par exemple, il existe des suites de rationnels qui sont de Cauchy mais qui ne convergent pas dans ℚ. |
| + | |||
| + | |||
| + | |||
| + | ===Complétude=== | ||
| + | On parle de '''complétude''' en mathématiques dans des sens très différents. On dit d'un objet mathématique qu'il est ''complet'' pour exprimer que rien ne peut lui être ajouté, en un sens qu'il faut préciser dans chaque contexte. Dans le cas contraire, on parle d''''incomplétude''', surtout dans le contexte de la logique mathématique. | ||
| + | |||
| + | * Un espace métrique est ''complet'' quand toute suite de Cauchy d'éléments de cet espace converge. | ||
==Théorie des Groupes== | ==Théorie des Groupes== | ||
| + | |||
| + | ===Groupe=== | ||
| + | En mathématiques, un groupe est un ensemble muni d'une loi de composition interne associative admettant un élément neutre et, pour chaque élément de l'ensemble, un élément symétrique. | ||
| + | |||
| + | Noté <math>(G,*)</math> | ||
| + | |||
| + | |||
| + | ===Groupe Abélien=== | ||
| + | Groupe requérant que sa loi de composition interne soit commutative. | ||
| + | |||
| + | ====Exemples==== | ||
| + | * <math>(\mathbb{Z},+)</math> est un groupe abélien; | ||
| + | * <math>(\mathbb{M}[\mathbb{R}], . )</math>, le groupe des matrices dans <math>\mathbb{R}</math> muni de la multiplication n'est pas commutatif : ça n'est pas un groupe abélien. | ||
| + | |||
| + | |||
| + | ===Anneau (Ring)=== | ||
| + | Groupe à 2 opérations, communément appelées ''addition'' et ''multiplication'' (cf. [http://www.youtube.com/watch?v=syHBApgJhsA&list=PLZzHxk_TPOStgPtqRZ6KzmkUQBQ8TSWVX cours #17 de Bill Shillito]) | ||
| + | |||
| + | [[File:Groups_-_Ring.png|500px]] | ||
| + | |||
| + | L'addition et la multiplication doivent être reliées entre elles par la ''propriété de distribution'' : | ||
| + | |||
| + | <math>a.(b+c) = a.b + a.c | ||
| + | </math> | ||
| + | |||
| + | ===Corps commutatif (Field)=== | ||
| + | Anneau où la multiplication est commutative. Le groupe formé par l'ensemble et la multiplication est un groupe abélien. | ||
| + | |||
| + | [[File:Groups - Field.png|500px]] | ||
| + | |||
| + | |||
| + | Remarque intéressante sur l'ensemble complexe qui forme un corps algébriquement fermé puisqu'il permet d'exprimer toutes les solutions de l'ensemble des polynômes <math>\mathbb{C}[x]</math> : | ||
| + | |||
| + | [[File:Groups - Complex Field.png|500px]] | ||
| + | |||
| + | |||
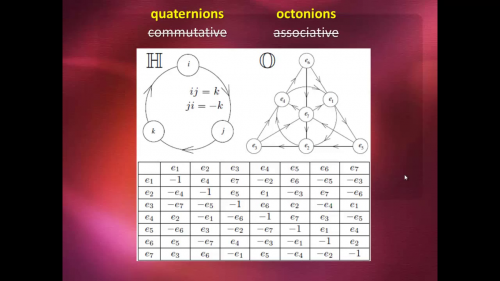
| + | ====Note sur les quaternions & octonions==== | ||
| + | Les quaternions perdent la propriété de commutativité de la multiplication. | ||
| + | |||
| + | Les octonions perdent les propriétés de commutativité '''et''' d'associativité de la multiplication. | ||
| + | |||
| + | [[File:Groups - Quaternions Octonions.png|500px]] | ||
Latest revision as of 16:48, 7 September 2013
Je vais tenter de me ré-initier à une catégorie des mathématiques que mes profs de math-sup m'avaient fait détester: l'algèbre. Et plus particulièrement, la théorie des groupes.
Comme c'est souvent le cas avec les sujets qu'on me force à ingurgiter, je mets un points d'honneur à n'en rien retenir. Je vais donc tout reprendre de zéro... Ces pages me serviront de notes de lecture et suivront l'ordre dans lequel je me serai de nouveau familiarisé avec ce sujet.
Contents
Bases
Axiome, Théorie Axiomatique
(http://fr.wikipedia.org/wiki/Axiome)
Un axiome (du grec ancien αξιωμα/axioma, « considéré comme digne, convenable, évident en soi » – lui-même dérivé de αξιος (axios), signifiant « digne ») désigne une vérité indémontrable qui doit être admise. Pour certains philosophes grecs de l'Antiquité, un axiome était une affirmation qu'ils considéraient comme évidente et qui n'avait nul besoin de preuve.
L'ensemble des axiomes d'une théorie est appelé axiomatique ou théorie axiomatique. Cette axiomatique définit la théorie ; ce qui signifie que l'axiome ne peut être remis en cause à l'intérieur de cette théorie, on dit alors que cette théorie est consistante. Un axiome représente donc plutôt un point de départ dans un système de logique et il peut être choisi arbitrairement. La pertinence d'une théorie dépend de la pertinence de ses axiomes et de son interprétation. En réalité, c'est de la non cohérence de son interprétation que vient la réfutation de la théorie non contradictoire et, par voie de conséquence, de son axiomatique. L'axiome est donc à la logique mathématique, ce qu'est le postulat à la physique théorique.
Exemple
on peut définir une arithmétique simple, comprenant un ensemble de « nombres » et une loi de composition, +, interne à cet ensemble, en posant (en s'inspirant un peu de Peano) :
- un nombre noté 0 existe
- tout nombre X a un successeur noté succ(X)
- X+0 = X
- succ(X) + Y = X + succ(Y)
A l'aide de ces axiomes on peut démontrer que succ(X) = X+1 puisque d'après 3) et 4) succ(X)+0 = X+succ(0) = X+1
Théorème
(http://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me)
Un théorème est une proposition qui peut être mathématiquement démontrée, c'est-à-dire une assertion qui peut être établie comme vraie au travers d'un raisonnement logique construit à partir d'axiomes.
Un théorème a généralement :
- des hypothèses de base, i.e. des conditions qui peuvent être énumérées dans le théorème ou décrites d'avance,
- une conclusion, i.e. une affirmation mathématique qui est vraie sous les conditions de base.
La démonstration, bien que nécessaire à la classification de la proposition comme « théorème », n'est pas considérée comme faisant partie du théorème. La démonstration comprend :
- des axiomes ;
- les hypothèses du théorème ;
- d'autres théorèmes déjà démontrés.
Chaque étape de la preuve est liée aux précédentes par des règles d'inférence logiques.
D'autres formes d'assertions
Au sens large toute assertion effectivement démontrée peut prendre le nom de théorème. Dans les ouvrages de mathématiques, il est cependant d'usage de réserver ce terme aux affirmations considérées comme nouvelles ou particulièrement intéressantes ou importantes. Selon leur importance, ou leur utilité, les autres assertions peuvent prendre des noms différents :
- lemme : assertion servant d'intermédiaire pour démontrer un théorème plus important ;
- corollaire : résultat qui découle directement d’un théorème prouvé ; on trouve aussi, dans les ouvrages anciens, le terme scholie. (Voir wikt:corollaire)
- proposition : résultat relativement simple qui n'est pas associé avec un théorème particulier ;
- remarque : résultat intéressant ou conséquence qui peut faire partie de la preuve ou d'une autre affirmation ;
- conjecture : proposition mathématique dont on ignore la valeur de vérité. Une fois prouvée, une conjecture devient un théorème.
Ensemble
(http://fr.wikipedia.org/wiki/Ensemble)
Un ensemble désigne intuitivement une collection d’objets (les éléments de l'ensemble), « une multitude qui peut être comprise comme un tout » (au sens d'omnis).
Dans une approche axiomatique, la théorie des ensembles est une théorie de l'appartenance (un élément d'un ensemble est dit « appartenir » à cet ensemble). Le mot ensemble désigne alors un objet du domaine de cette théorie, dont les axiomes régissent les propriétés. La théorie des ensembles est utilisée pour fonder les mathématiques, et dans cette approche tout objet mathématique est in fine un ensemble.
La formulation en reviendrait au mathématicien Georg Cantor, qui énonçait : « Par ensemble, nous entendons toute collection M d'objets m de notre intuition ou de notre pensée, définis et distincts, ces objets étant appelés les éléments de M »
Les éléments peuvent être de n’importe quelle nature : nombres, points géométriques, droites, fonctions, autres ensembles...
L'appartenance d'un élément, noté par exemple x, à un ensemble, noté par exemple A, s’écrit : x ∈ A.
On dira donc que deux ensembles A et B sont égaux (on le notera comme d'habitude A = B) quand ils ont exactement les mêmes éléments. Cette propriété est connue sous le nom d'extensionnalité :
A = B si et seulement si ∀x (x ∈ A ⇔ x ∈ B) où « ⇔ » désigne l'équivalence logique.
Exemples
- L'ensemble auxquels appartiennent les éléments 2, 3, et 5, et seulement ces éléments, est noté {2, 3, 5}. L'ensemble est défini en extension.
- La façon la plus générale de définir un ensemble est de donner une propriété caractéristique des éléments de cet ensemble. Par exemple, on pourra définir l'ensemble des nombres premiers par une propriété caractéristique de ceux-ci : être différent de 1 et avoir pour seuls diviseurs 1 et lui-même. On parle de définition en compréhension.
- Par extensionnalité, il n'y a qu'un seul ensemble sans éléments, l'ensemble vide, que l'on note ∅ ou { }.
- L'ensemble des entiers naturels pairs : <math>\{x \in\mathbb{N}\mid x\ \rm pair \}</math>.
- On définira de la même façon (ℤ désignant l'ensemble des entiers relatifs) :
- <math>\{x \in\mathbb{Z}\mid -7 \leq x \leq 23\}</math> l'ensemble des entiers relatifs compris entre -7 et 23 ;
- <math>\left\{x \in\mathbb{N}\mid \exists y \in \mathbb{N}\ (y \geq 1\ {\rm et}\ x = y^2)\right\}</math> l'ensemble des carrés parfaits non nuls.
Intervalle
En mathématiques, un intervalle (du latin intervallum) est étymologiquement un ensemble compris entre deux valeurs. Cette notion première s'est ensuite développée jusqu'à aboutir aux définitions suivantes.
Initialement, on appelle intervalle réel un ensemble de nombres délimité par deux nombres réels constituant une borne inférieure et une borne supérieure. Un intervalle contient tous les nombres réels compris entre ces deux bornes.
Cette définition regroupe les intervalles des types suivants (avec <math>(a,b)\in\mathbb{R}^2,\ a<b</math>):
- <math>\{x\in\mathbb{R} \mid a < x < b \} = \;]a; b[</math> (ouvert et non fermé)
- <math>\{x\in\mathbb{R} \mid a \leq x \leq b \} = [a ; b]</math> (fermé et non ouvert)
- <math>\{x\in\mathbb{R} \mid a < x \leq b \} = \;]a; b]</math> (ni ouvert, ni fermé)
- <math>\{x\in\mathbb{R} \mid a \leq x < b \} = [a; b[</math> (ni ouvert, ni fermé)
Les intervalles du premier type sont appelés intervalles ouverts ; les seconds intervalles fermés, et les deux derniers intervalles semi-ouverts.
Union et intersection
- Une intersection d'intervalles de <math>\mathbb{R}</math> est toujours un intervalle.
- Une union d'intervalles de <math>\mathbb{R}</math> n'est pas toujours un intervalle. Ce sera un intervalle si l'ensemble obtenu reste convexe (intuitivement s'il n'y a pas de "trou"). Dans le cas d'une union de deux intervalles, il suffit que l'intersection de ces intervalles soit non vide pour que leur réunion soit convexe.
En analyse et en topologie
Les intervalles sont les parties de <math>\mathbb{R}</math> les plus intéressantes dès que l'on parle de continuité et de dérivabilité.
On trouve alors (entre autres) pour les fonctions réelles d'une variable réelle, des propriétés telles que :
- L'image par une fonction continue d'un intervalle de <math>\mathbb{R}</math> est un intervalle de <math>\mathbb{R}</math> (théorème des valeurs intermédiaires)
- Une fonction dérivable et à dérivée identiquement nulle sur un intervalle est constante sur cet intervalle.
- Une fonction dérivable est monotone sur un intervalle si et seulement si sa dérivée garde un signe constant sur cet intervalle
Loi de Composition Interne
Une loi de composition interne (ou, parfois, opération) est un procédé qui, à deux éléments d'un ensemble E, associe un troisième élément de E. L'addition et la multiplication sont des exemples classiques de lois de composition interne des ensembles de nombres usuels, tels que les entiers naturels.
Nous avons tous depuis le primaire une assez bonne idée de la notion d'opérations telles que l'addition, la soustraction, la multiplication ou la division. Une opération (interne) dans un ensemble est une relation interne dans cet ensemble, qui, à deux éléments quelconques de cet ensemble, appelés opérandes, en associe éventuellement un troisième, unique, nommé résultat, toujours dans ce même ensemble.
Pour que l’opération considérée soit effectivement une loi de composition interne, il faut qu’elle ait un sens quels que soient les deux éléments de l’ensemble choisis (on dit formellement que l'opération doit être définie partout). Ainsi :
- la division n’est pas une loi de composition interne dans <math>\mathbb{R} \,,</math> parce qu’on ne peut pas diviser par zéro : par exemple, « 3 / 0 » n’a pas de sens. Mais cette même division est une loi de composition interne dans <math>\mathbb{R}^{*} \,</math> (ensemble des réels privés de 0). Enfin cette même opération n'est pas une loi de composition interne dans <math>\mathbb{Z}^{*} \,</math> car 2 / 3 n'est pas un entier relatif.
- la soustraction peut être ou non une loi de composition interne selon l’ensemble de nombres considéré :
- s’il s’agit de l’ensemble des nombres usuels, dits entiers naturels { 0, 1, 2, 3,... }, ce n’en est pas une, puisque « 3 - 5 », par exemple, n’a pas pour résultat l’un de ces nombres usuels.
- si au contraire, on choisit l’ensemble des entiers relatifs, qui en plus des entiers naturels, contient les entiers négatifs { ..., -3, -2, -1}, alors la soustraction est bien une loi de composition interne.
En résumé, une loi de composition interne dans un ensemble E, ou, plus simplement une loi dans E, est une opération qui donne un résultat dans E pour tous les couples possibles d'éléments de E.
Exemple
Dans l’ensemble des entiers relatifs, l’addition est une loi de composition interne ayant entre autres les propriétés suivantes, qui seront définies plus formellement dans la seconde partie de l’article :
- 0 est élément neutre pour cette loi : l’ajouter à n’importe quel nombre redonne ce nombre : par exemple, 5 + 0 = 5 , et 0 + 8 = 8 ;
- pour tout entier, il existe un autre nombre, son opposé (le terme général est élément symétrique), tel qu’ajouté au premier, il redonne l’élément neutre 0. L’opposé se note comme l’entier initial changé de signe. Ainsi : 3 + (-3) = 0 ;
- on peut échanger les deux éléments autour du signe « <math>+</math> » : 3 + 5 = 5 + 3 = 8 . On dit que l’opération est commutative ;
- on peut grouper les éléments comme on le souhaite quand on en ajoute plus de deux : 3 + 5 + 4 peut se calculer de deux manières :
- en calculant d’abord 3 + 5 = 8 puis en ajoutant 4 au résultat,
- ou en calculant 5 + 4 = 9 avant de calculer 3 + 9 .
- Ces deux méthodes mènent au même résultat, ce que l’on note : (3 + 5) + 4 = 3 + (5 + 4) . On dit que l’opération est associative.
Ces quatre propriétés, existence d’un élément neutre, existence de symétriques, commutativité, associativité, peuvent se retrouver pour d’autres ensembles et d’autres lois. Ainsi, on peut étudier l’ensemble des translations (c’est-à-dire les déplacements en ligne droite : par exemple, se déplacer de 3 mètres vers la gauche et de 2 mètres vers le haut), et une loi de composition interne sur cet ensemble, la composition : la composition de deux translations consistant simplement à faire le premier déplacement, puis le second. On retrouve pour la composition les mêmes propriétés que pour l’addition :
- le neutre est la translation nulle, consistant à ne pas se déplacer ;
- le symétrique d’une translation consiste à faire le même déplacement dans l’autre sens (3 mètres à droite et 2 mètres vers le bas pour l’exemple précédent) : si on fait successivement les deux, c’est comme si on faisait le déplacement nul ;
- on peut faire les déplacements dans l’ordre qu’on veut, on retrouve la commutativité et l’associativité.
Suite réelle ou complexe de Cauchy
Une suite de réels ou de complexes <math>(r_n) \ </math> est dite de Cauchy, ou vérifie le critère de Cauchy, lorsque les termes de la suite se rapprochent uniformément les uns des autres en l'infini au sens où :
Cette dernière condition se réécrit classiquement à l'aide de quantificateurs universels et existentiels :
L'uniformité dans la définition est importante. En effet, la différence des termes consécutifs de la suite <math>(\ln(n)) \ </math> tend vers 0, et, plus précisément :
Cependant, <math>\ln(2n)-\ln(n)=\ln(2) \ </math> ne converge pas vers 0 lorsque n tend vers l'infini. La suite n'est donc pas de Cauchy.
Critère de Cauchy : Une suite <math>(r_n) \ </math> de nombres réels (respectivement complexes) converge dans ℝ (respectivement ℂ) si et seulement si c'est une suite de Cauchy.
Suite de Cauchy dans un espace métrique
Une suite <math>(x_n)_{n\in\N}</math> dans un espace métrique <math>(E,d)</math> est dite suite de Cauchy (ou de Cauchy) si pour tout réel <math>\varepsilon>0</math>, il existe un entier naturel <math>N</math> tel que pour tous entiers <math>p,q\geq N</math>, la distance <math>d(x_p,x_q)</math> soit inférieure à <math>\varepsilon</math> :
ou plus synthétiquement, si
ou encore :
Les inégalités autres que <math>\varepsilon>0</math> peuvent être prises indifféremment larges ou strictes. Lorsque certains ouvrages introduisent la notion de suite de Cauchy uniquement pour les suites de réels, c'est exactement la même définition. La distance d est simplement à remplacer par la valeur absolue de la différence.
Intuitivement, les termes de la suite deviennent de plus en plus proches les uns des autres d'une certaine façon qui suggère que la suite doit avoir une limite dans l'espace. Les suites convergentes sont effectivement de Cauchy, mais néanmoins la réciproque n'est pas vraie en toute généralité. Par exemple, il existe des suites de rationnels qui sont de Cauchy mais qui ne convergent pas dans ℚ.
Complétude
On parle de complétude en mathématiques dans des sens très différents. On dit d'un objet mathématique qu'il est complet pour exprimer que rien ne peut lui être ajouté, en un sens qu'il faut préciser dans chaque contexte. Dans le cas contraire, on parle d'incomplétude, surtout dans le contexte de la logique mathématique.
- Un espace métrique est complet quand toute suite de Cauchy d'éléments de cet espace converge.
Théorie des Groupes
Groupe
En mathématiques, un groupe est un ensemble muni d'une loi de composition interne associative admettant un élément neutre et, pour chaque élément de l'ensemble, un élément symétrique.
Noté <math>(G,*)</math>
Groupe Abélien
Groupe requérant que sa loi de composition interne soit commutative.
Exemples
- <math>(\mathbb{Z},+)</math> est un groupe abélien;
- <math>(\mathbb{M}[\mathbb{R}], . )</math>, le groupe des matrices dans <math>\mathbb{R}</math> muni de la multiplication n'est pas commutatif : ça n'est pas un groupe abélien.
Anneau (Ring)
Groupe à 2 opérations, communément appelées addition et multiplication (cf. cours #17 de Bill Shillito)
L'addition et la multiplication doivent être reliées entre elles par la propriété de distribution :
<math>a.(b+c) = a.b + a.c </math>
Corps commutatif (Field)
Anneau où la multiplication est commutative. Le groupe formé par l'ensemble et la multiplication est un groupe abélien.
Remarque intéressante sur l'ensemble complexe qui forme un corps algébriquement fermé puisqu'il permet d'exprimer toutes les solutions de l'ensemble des polynômes <math>\mathbb{C}[x]</math> :
Note sur les quaternions & octonions
Les quaternions perdent la propriété de commutativité de la multiplication.
Les octonions perdent les propriétés de commutativité et d'associativité de la multiplication.