| Line 48: | Line 48: | ||
The expression of vector V in cartesian coordinates is <math>v(\phi,\theta) = (sin(\theta)cos(\phi), sin(\theta)sin(\phi), cos(\theta))</math>. | The expression of vector V in cartesian coordinates is <math>v(\phi,\theta) = (sin(\theta)cos(\phi), sin(\theta)sin(\phi), cos(\theta))</math>. | ||
| − | |||
| − | <math>Y^m_l(\theta,\phi) = K^m_l P^m_l(\theta | + | The general spherical harmonics coefficient <math>Y^m_l(\theta,\phi)</math> is expressed as:<br /> |
| + | :<math>Y^m_l(\theta,\phi) = K^m_l P^m_l(cos(\theta)) e^{im\phi}</math><br /> | ||
| − | Where <math>K^m_l = \sqrt{ \frac{(2l+1)}{4\pi}\frac{(l-m)!}{(l+m)!}}</math> is a normalization factor. | + | Where <math>K^m_l = \sqrt{ \frac{(2l+1)}{4\pi}\frac{(l-m)!}{(l+m)!}}</math> is a normalization factor and <math>P^m_l(\theta,\phi)</math> is the [https://en.wikipedia.org/wiki/Associated_Legendre_polynomials associated Legendre polynomial].<br /> |
| + | <br /> | ||
| + | We're interested in the ''real form'' of spherical harmonics that is given by:<br /> | ||
| + | :<math> | ||
| + | \begin{cases} | ||
| + | \sqrt{2} K^{-m}_l P^{-m}_l(cos(\theta)) sin(-m\phi) & \quad \text{if } m < 0\\ | ||
| + | K^0_l P^0_l(cos(\theta)) & \quad \text{if } m = 0\\ | ||
| + | \sqrt{2} K^m_l P^{| m |}_l(cos(\theta)) cos(m\phi) & \quad \text{if } m > 0\\ | ||
| + | \end{cases} | ||
| + | </math> | ||
Revision as of 20:05, 2 December 2016
This page serves as an entry point to everything related to Spherical Harmonics.
Contents
What are Spherical Harmonics (SH)?
According to wikipedia, SH are special functions defined on the surface of a sphere.
In computer graphics, we're using them as a tool to quickly and easily encode or decode a directional information. We use a specific set of spherical harmonics, denoted <math>Y^m_l(\theta,\phi)</math> called Laplace's spherical harmonics.
SH have interesting properties regarding their orthogonality, parity, symmetry and rotation that I will not cover here (cf. the wikipedia page for more info) as this page only is an overview. An excellent source of information is Spherical Harmonics Lighting: the Gritty Details by Robin Green that actually covers the practical use of SH for Computer Graphics, it's a well-explained extension of the original work done by Peter Pike Sloane who is pretty much the guy who introduced SH to Computer Graphics for Pre-computed Radiance Transfer (PRT).
I will rather quickly talk about how to construct the SH coefficients and how to encode/decode/convolve signals using SH.
Generalities about SH orders
As can be seen in the inset on the right, Spherical Harmonics are functions defined over the sphere. They are denoted <math>Y^m_l(\theta,\phi)</math> where <math>l</math> is the order of the coefficient. Since SH define harmonic series, there are an infinite amount of possible orders.
For a given order <math>l</math> you have <math>2l+1</math> coefficients selected by the superscript <math>m\in[-l,+l]</math>. It ensues that the amount of coefficients for each order is then:
1 Order 0 - Total = 1 = 1²
2 3 4 Order 1 - Total = 1 + 3 = 4 = 2²
5 6 7 8 9 Order 2 - Total = 1 + 3 + 5 = 9 = 3²
10 11 12 13 14 15 16 Order 3 - Total = 1 + 3 + 5 + 9 = 16 = 4²
<math>\dots</math>
We quickly see the amount of coefficients to properly represent each order grows quadratically.
Intuitively, we also can notice that the more coefficients we have, the more "directionalities" we can cover. Order 0 is a constant so it represents the "ambient term", the average response of a signal and has no specific direction. Coefficients for order 1 represent the response to a signal aligned with the X, Y and Z axes. At order 2, we start covering some diagonal directions and higher frequencies.
In fact, if we used an infinite sum of SH coefficients, we could encode or decode a signal perfectly. A great advantage of using SH is that we can recover a partial signal (i.e. a band-limited signal) and we will obtain a low-frequency representation of that signal, as opposed to wavelets that attempt to reconstruct all frequencies of a signal and can show high-frequency noise, a partial SH-encoded signal will always be smooth.
It is common in real-time computer graphics to use only order 2 (9 coefficients) or order 3 (16 coefficients) at most, each coefficient being a RGB float3 triplet. SH are often used to encode irradiance, which is generally spatially varying pretty smoothly. It's also possible to encode radiance, although it varies at higher frequency than irradiance, since irradiance is simply the convolution of radiance on the entire hemisphere in a particular direction.
A great paper from Ramamoorthi and Hanrahan from 2001 shows the relationship between radiance and irradiance in terms of SH. It was shortly followed by another seminal paper called "An Efficient Representation for Irradiance Environment Maps" that extends on the first paper and shows that order 2 SH (9 coefficients) is often enough to properly represent the irradiance field surrounding an object since additional order disappear very quickly. We will come back to these papers later as I will show an extension on this irradiance estimate to introduce the Ambient Occlusion term.
Constructing the SH coefficients
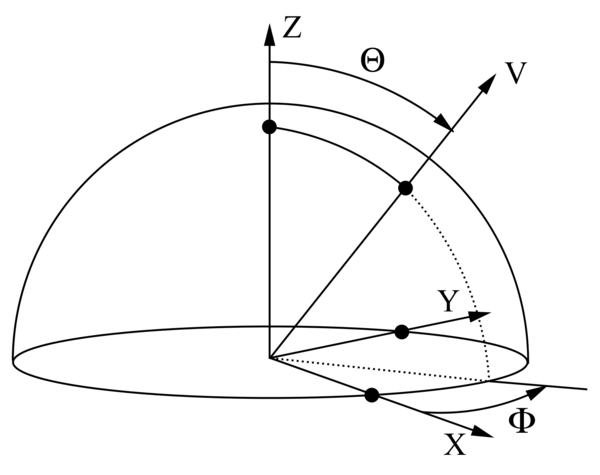
We're working with a Z-Up orientation:
The expression of vector V in cartesian coordinates is <math>v(\phi,\theta) = (sin(\theta)cos(\phi), sin(\theta)sin(\phi), cos(\theta))</math>.
The general spherical harmonics coefficient <math>Y^m_l(\theta,\phi)</math> is expressed as:
- <math>Y^m_l(\theta,\phi) = K^m_l P^m_l(cos(\theta)) e^{im\phi}</math>
Where <math>K^m_l = \sqrt{ \frac{(2l+1)}{4\pi}\frac{(l-m)!}{(l+m)!}}</math> is a normalization factor and <math>P^m_l(\theta,\phi)</math> is the associated Legendre polynomial.
We're interested in the real form of spherical harmonics that is given by:
- <math>
\begin{cases}
\sqrt{2} K^{-m}_l P^{-m}_l(cos(\theta)) sin(-m\phi) & \quad \text{if } m < 0\\
K^0_l P^0_l(cos(\theta)) & \quad \text{if } m = 0\\
\sqrt{2} K^m_l P^{| m |}_l(cos(\theta)) cos(m\phi) & \quad \text{if } m > 0\\
\end{cases} </math>
Archive
You can find an old (2009) explanation about SH Environment Maps.