Contents
Matrix Decomposition Methods
QR Decomposition
QR Decomposition, or QR Factorization is the process of decomposing a matrix A this way: <math>\left [ \bold{A} \right ] = \left [ \bold{Q} \right ] \cdot \left [ \bold{R} \right ]</math>
Where:
- Q is an orthogonal matrix
- R is an upper triangular matrix
Applications
QR decomposition is often used to solve the linear least squares problem, and is the basis for a particular eigenvalue algorithm, the QR algorithm.
SVD Decomposition
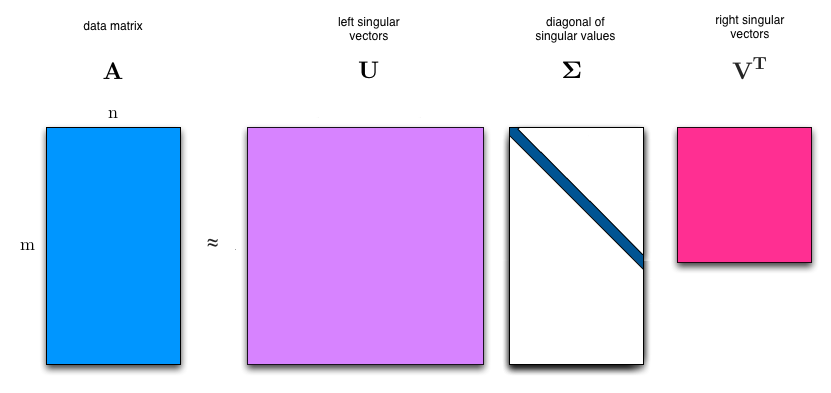
Singular Value Decomposition (SVD) is the process of decomposing a matrix A this way:
<math>\left [ \bold{A} \right ] = \left [ \bold{U} \right ] \cdot \left [ \bold{\Sigma} \right ] \cdot \left [ \bold{V} \right ]^T</math>
Where:
- A is an m by n real or complex matrix
- U is an m by n real or complex unitary matrix
- <math>\bold{\Sigma}</math> is a m by n rectangular diagonal matrix with non-negative real numbers on the diagonal
- V is an n by n real or complex unitary matrix.
The diagonal entries <math>\sigma_i</math> of <math>\bold{\Sigma}</math> are known as the singular values of A. The columns of U and the columns of V are called the left-singular vectors and right-singular vectors of A, respectively.
The singular value decomposition can be computed using the following observations:
- The left-singular vectors of M are a set of orthonormal eigenvectors of <math>\bold{A}\bold{A}^T</math>.
- The right-singular vectors of M are a set of orthonormal eigenvectors of <math>\bold{A}^T\bold{A}</math>.
- The non-zero singular values of M (found on the diagonal entries of Σ) are the square roots of the non-zero eigenvalues of both <math>\bold{A}^T\bold{A}</math> and <math>\bold{A}\bold{A}^T</math>.
Applications
Applications that employ the SVD include computing the pseudoinverse, least squares fitting of data, multivariable control, matrix approximation, and determining the rank, range and null space of a matrix.