| Line 24: | Line 24: | ||
As it is well-known to shader programmers, computing the cross product of these vectors gives us the normal to the sphere at this position <math>x, y</math> on the plane, and the length of that normal is the tiny area element <math>dA</math> on the hemisphere. | As it is well-known to shader programmers, computing the cross product of these vectors gives us the normal to the sphere at this position <math>x, y</math> on the plane, and the length of that normal is the tiny area element <math>dA</math> on the hemisphere. | ||
| − | Integrating this operation (cross product and norm computation) over an interval <math>[a,b]\in\mathbb{R}</math> yields: | + | Integrating this operation (cross product and norm computation) over an interval <math>[a,b]\in\mathbb{R}^2</math> yields: |
<math>A(a,b) = \int_0^b{\int_0^a{ \left | \frac{\partial \mathbf{p}}{\partial x} \times \frac{\partial \mathbf{p}}{\partial y} \right | dx} dy} \quad | <math>A(a,b) = \int_0^b{\int_0^a{ \left | \frac{\partial \mathbf{p}}{\partial x} \times \frac{\partial \mathbf{p}}{\partial y} \right | dx} dy} \quad | ||
| Line 30: | Line 30: | ||
= \left | atan( \frac{xy}{\sqrt{1+x^2+y^2}} ) \right | | = \left | atan( \frac{xy}{\sqrt{1+x^2+y^2}} ) \right | | ||
</math> | </math> | ||
| + | |||
| + | It's easy to notice that <math>A(1,1) = \frac{\pi}{6}</math> which is the solid angle covered by a quarter of our cube map face, the solid angle of an entier face would be <math>\frac{2\pi}{3}</math> and all 6 faces of the cube map are then covering a proper solid angle of <math>4\pi</math> and all is well! | ||
| + | |||
| + | Now, for our little problem... | ||
==Our Projection Configuration== | ==Our Projection Configuration== | ||
| + | |||
| + | Our configuration is a little bit different as our points <math>\mathbf{p'}(x,y) = (x,y,0)</math> and we project onto the hemisphere to obtain <math>\mathbf{p}(x,y) = (x,y,\sqrt{1-x^2-y^2})</math>. | ||
| + | |||
| + | The partial derivatives along x and y give: | ||
| + | |||
| + | <math>\frac{\partial \mathbf{p}}{\partial x} = \begin{pmatrix} 1 \\ 0 \\ -\frac{x}{\sqrt{1-x^2-y^2}} \end{pmatrix}</math> | ||
| + | |||
| + | <math>\frac{\partial \mathbf{p}}{\partial y} = \begin{pmatrix} 0 \\ 1 \\ -\frac{y}{\sqrt{1-x^2-y^2}} \end{pmatrix}</math> | ||
| + | |||
| + | |||
| + | The cross product of these 2 vectors gives: | ||
| + | |||
| + | <math>\frac{\partial \mathbf{p}}{\partial x} \times \frac{\partial \mathbf{p}}{\partial y} = \frac{1}{\sqrt{1-x^2-y^2}} \begin{pmatrix} x \\ y \\ \sqrt{1-x^2-y^2} \end{pmatrix}</math> | ||
| + | |||
| + | |||
| + | And the norm is: | ||
| + | |||
| + | <math>\left | \frac{\partial \mathbf{p}}{\partial x} \times \frac{\partial \mathbf{p}}{\partial y} \right | = \frac{1}{\sqrt{1-x^2-y^2}}</math> | ||
| + | |||
| + | |||
| + | Which looks kinda nice! Integrating <math>\int_0^1\int_0^1 \frac{1}{\sqrt{1-x^2-y^2}} dx dy = \frac{\pi}{2}</math> which is a quarter of the entire hemisphere's solid angle <math>2\pi</math>, so we're good! | ||
Revision as of 19:33, 2 June 2017
Hi!
Maybe you already bumped into the problem of projecting a cubemap into spherical harmonics and found this page to help you out: http://www.rorydriscoll.com/2012/01/15/cubemap-texel-solid-angle/ ?
But maybe you need the solution to another, similar problem that consists in finding the solid angle of a pixel lying in the z=0 plane and orthogonally projected onto the hemisphere, but couldn't find a page with that computation?
Well let me help you with that! ![]()
First of all, the document that was used initially to do the computations, both in AMD's cube map generator, Rory Driscoll's summary and this page, is the very interesting thesis by Manne Öhrström.
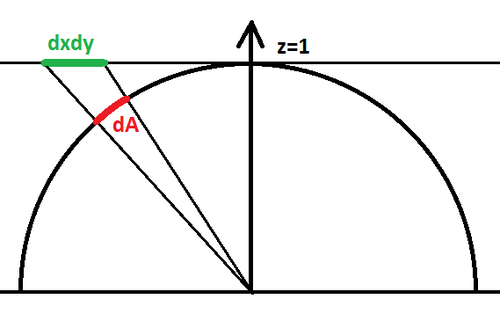
Cubemap Projection Configuration
The configuration for a cube map is that pixels are lying on a plane z=1 such as <math>\mathbf{p'}=(x,y,1), -1<x<1, -1<y<1</math> and we project back onto the unit hemisphere by "normalizing" the vector <math>\mathbf{p}=\frac{\mathbf{p'}}{|\mathbf{p'}|}=\frac{(x,y,1)}{\sqrt{1+x^2+y^2}}</math> as shown on the figure below:
The idea is to compute the area of a small element of surface on the hemisphere as we make it vary on the plane, we do that by computing the partial derivatives of <math>\mathbf{p}</math> along x and y that give us the vectors <math>\frac{\partial \mathbf{p}}{\partial x}</math> and <math>\frac{\partial \mathbf{p}}{\partial y}</math>.
As it is well-known to shader programmers, computing the cross product of these vectors gives us the normal to the sphere at this position <math>x, y</math> on the plane, and the length of that normal is the tiny area element <math>dA</math> on the hemisphere.
Integrating this operation (cross product and norm computation) over an interval <math>[a,b]\in\mathbb{R}^2</math> yields:
<math>A(a,b) = \int_0^b{\int_0^a{ \left | \frac{\partial \mathbf{p}}{\partial x} \times \frac{\partial \mathbf{p}}{\partial y} \right | dx} dy} \quad = \int_0^b{\int_0^a{(1+x^2+y^2)^{-\frac{3}{2}} dx} dy} \quad = \left | atan( \frac{xy}{\sqrt{1+x^2+y^2}} ) \right | </math>
It's easy to notice that <math>A(1,1) = \frac{\pi}{6}</math> which is the solid angle covered by a quarter of our cube map face, the solid angle of an entier face would be <math>\frac{2\pi}{3}</math> and all 6 faces of the cube map are then covering a proper solid angle of <math>4\pi</math> and all is well!
Now, for our little problem...
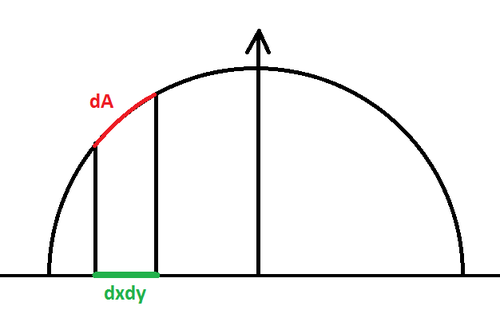
Our Projection Configuration
Our configuration is a little bit different as our points <math>\mathbf{p'}(x,y) = (x,y,0)</math> and we project onto the hemisphere to obtain <math>\mathbf{p}(x,y) = (x,y,\sqrt{1-x^2-y^2})</math>.
The partial derivatives along x and y give:
<math>\frac{\partial \mathbf{p}}{\partial x} = \begin{pmatrix} 1 \\ 0 \\ -\frac{x}{\sqrt{1-x^2-y^2}} \end{pmatrix}</math>
<math>\frac{\partial \mathbf{p}}{\partial y} = \begin{pmatrix} 0 \\ 1 \\ -\frac{y}{\sqrt{1-x^2-y^2}} \end{pmatrix}</math>
The cross product of these 2 vectors gives:
<math>\frac{\partial \mathbf{p}}{\partial x} \times \frac{\partial \mathbf{p}}{\partial y} = \frac{1}{\sqrt{1-x^2-y^2}} \begin{pmatrix} x \\ y \\ \sqrt{1-x^2-y^2} \end{pmatrix}</math>
And the norm is:
<math>\left | \frac{\partial \mathbf{p}}{\partial x} \times \frac{\partial \mathbf{p}}{\partial y} \right | = \frac{1}{\sqrt{1-x^2-y^2}}</math>
Which looks kinda nice! Integrating <math>\int_0^1\int_0^1 \frac{1}{\sqrt{1-x^2-y^2}} dx dy = \frac{\pi}{2}</math> which is a quarter of the entire hemisphere's solid angle <math>2\pi</math>, so we're good!