| Line 63: | Line 63: | ||
The integration of radiance arriving at a surface element <math>dA</math>, times <math>n.\omega_i</math> yields the irradiance (<math>W.m^{-2}</math>): | The integration of radiance arriving at a surface element <math>dA</math>, times <math>n.\omega_i</math> yields the irradiance (<math>W.m^{-2}</math>): | ||
| − | <math>E_r(x) = \int_\Omega dE_i(x,\omega_i) = \int_\Omega L_i(x,\omega_i) (n.\omega_i) \, d\omega_i~~~~~~~~~\mbox{(1)}</math> | + | :<math>E_r(x) = \int_\Omega dE_i(x,\omega_i) = \int_\Omega L_i(x,\omega_i) (n.\omega_i) \, d\omega_i~~~~~~~~~\mbox{(1)}</math> |
It means that by summing the radiance (<math>W.m^{-2}.sr^{-1}</math>) coming from all possible directions, we get rid of the angular component (the <math>sr^{-1}</math> | It means that by summing the radiance (<math>W.m^{-2}.sr^{-1}</math>) coming from all possible directions, we get rid of the angular component (the <math>sr^{-1}</math> | ||
| Line 77: | Line 77: | ||
So, perhaps we could include the BRDF ''in front'' of the irradiance integral and obtain a radiance like this: | So, perhaps we could include the BRDF ''in front'' of the irradiance integral and obtain a radiance like this: | ||
| − | <math>L_r(x,\omega_o) = f_r(x,\omega_o) \int_\Omega L_i(\omega_i) (n.\omega_i) \, d\omega_i</math> | + | :<math>L_r(x,\omega_o) = f_r(x,\omega_o) \int_\Omega L_i(\omega_i) (n.\omega_i) \, d\omega_i</math> |
Well, it ''can'' work for a few cases. | Well, it ''can'' work for a few cases. | ||
| Line 97: | Line 97: | ||
When we inject the BRDF into the integral, we obtain a new radiance: | When we inject the BRDF into the integral, we obtain a new radiance: | ||
| − | <math>L_r(x,\omega_o) = \int_\Omega f_r(x,\omega_o,\omega_i) L_i(\omega_i) (n.\omega_i) \, d\omega_i~~~~~~~~~\mbox{(2)}</math> | + | :<math>L_r(x,\omega_o) = \int_\Omega f_r(x,\omega_o,\omega_i) L_i(\omega_i) (n.\omega_i) \, d\omega_i~~~~~~~~~\mbox{(2)}</math> |
We see that now <math>f_r(x,\omega_o,\omega_i)</math> is dependent on both <math>\omega_i</math> and <math>\omega_o</math> and becomes much more difficult to handle than our simple Lambertian factor from earlier. | We see that now <math>f_r(x,\omega_o,\omega_i)</math> is dependent on both <math>\omega_i</math> and <math>\omega_o</math> and becomes much more difficult to handle than our simple Lambertian factor from earlier. | ||
| Line 104: | Line 104: | ||
Anyway, we now integrate radiance multiplied by the BRDF. We saw from equation (1) that integrating without multiplying by the BRDF yields the irradiance, but when integrating with the multiplication by the BRDF, we obtain radiance so it's perfectly reasonable to assume that the expression of the BRDF is: | Anyway, we now integrate radiance multiplied by the BRDF. We saw from equation (1) that integrating without multiplying by the BRDF yields the irradiance, but when integrating with the multiplication by the BRDF, we obtain radiance so it's perfectly reasonable to assume that the expression of the BRDF is: | ||
| − | <math>f_r(x,\omega_o,\omega_i) = \frac{dL_r(x,\omega_o)}{dE_i(x,\omega_i)}~~~~~~~~~~~~\mbox{(which is simply radiance divided by irradiance)}</math> | + | :<math>f_r(x,\omega_o,\omega_i) = \frac{dL_r(x,\omega_o)}{dE_i(x,\omega_i)}~~~~~~~~~~~~\mbox{(which is simply radiance divided by irradiance)}</math> |
From equation (1) we find that: | From equation (1) we find that: | ||
| − | <math>dE_i(x,\omega_i) = L_i(x,\omega_i) (n.\omega_i) d\omega_i~~~~~~~~~~~~\mbox{(note that we simply removed the integral signs to get this)}</math> | + | :<math>dE_i(x,\omega_i) = L_i(x,\omega_i) (n.\omega_i) d\omega_i~~~~~~~~~~~~\mbox{(note that we simply removed the integral signs to get this)}</math> |
| Line 215: | Line 215: | ||
The general analytical model that is often used by the models listed above is called "microfacet model". It is written like this for isotropic materials: | The general analytical model that is often used by the models listed above is called "microfacet model". It is written like this for isotropic materials: | ||
| − | <math>f_r(x,\omega_o,\omega_i) = \mbox{diffuse} + \mbox{specular} = \mbox{diffuse} + \frac{F(\theta_d)G(\theta_i,\theta_o)D(\theta_h)}{4\cos\theta_i\cos\theta_o}</math> | + | :<math>f_r(x,\omega_o,\omega_i) = \mbox{diffuse} + \mbox{specular} = \mbox{diffuse} + \frac{F(\theta_d)G(\theta_i,\theta_o)D(\theta_h)}{4\cos\theta_i\cos\theta_o}</math> |
| Line 239: | Line 239: | ||
Disney uses an interesting variation of the Trowbridge-Reitz distribution that helps to compensate for the short tail problem: | Disney uses an interesting variation of the Trowbridge-Reitz distribution that helps to compensate for the short tail problem: | ||
| − | <math>D_\mathrm{generalizedTR}(\theta_h) = \frac{\alpha_\mathrm{tr}^2}{\pi(\alpha_\mathrm{tr}^2.\cos(\theta_h)^2 + sin(\theta_h)^2)^\gamma}</math> | + | :<math>D_\mathrm{generalizedTR}(\theta_h) = \frac{\alpha_\mathrm{tr}^2}{\pi(\alpha_\mathrm{tr}^2.\cos(\theta_h)^2 + sin(\theta_h)^2)^\gamma}</math> |
[[File:GeneralizedTrowbridge.jpg|600px]] | [[File:GeneralizedTrowbridge.jpg|600px]] | ||
| Line 265: | Line 265: | ||
[[File:BRDFPartsFresnel.jpg|thumb|right]] | [[File:BRDFPartsFresnel.jpg|thumb|right]] | ||
| − | The <math>F(\theta_d)</math> term is called the | + | The <math>F(\theta_d)</math> term is called the [http://en.wikipedia.org/wiki/Fresnel_equations "Fresnel Reflectance"] and models the amount of light that will effectively participate to the specular reflection (the rest of the incoming light entering the surface to participate to the diffuse effect). |
[[File:Fresnel.jpg|800px]] | [[File:Fresnel.jpg|800px]] | ||
| − | The | + | We immediately notice that: |
| + | * The Fresnel reflectance curves don't change much over most of the range, say from 0° (i.e. light/view is orthogonal to the surface) to ~60°, then the reflectance jumps to 1 (i.e. total reflection) at 90° which is quite intuitive since photons arriving at grazing angles have almost no chance of entering the material and almost all of them bounce off the surface. The Fresnel reflectance value when <math>\theta_d = 0°</math> (i.e. when viewing the surface perpendicularly) is called <math>F_0</math> and is often used as the ''characteristic specular reflectance'' of the material. It's very convenient as it can be represented by a RGB color in [0,1] and we can think of it as the "specular color" of the material. | ||
| − | <math>F(\theta_d) = | + | * Metals usually have a colored specular reflection while dielectric materials (e.g. water, glass) have a uniform specular and need only luminance encoding. |
| + | |||
| + | * Finally, we can notice (actually, I didn't notice that at all, I read it in one of the lectures [[File:S2.gif]]) that smooth materials generally have a Fresnel reflectance <math>F_0 < 0.5</math> while rough materials have a <math>F_0 > 0.5</math>. | ||
| + | |||
| + | |||
| + | The expressions for the [http://en.wikipedia.org/wiki/Fresnel_equations#Definitions_and_power_equations Fresnel reflectance] are quite complicated and deal with complex numbers but thanks to a simplification by [http://www.cs.virginia.edu/~jdl/bib/appearance/analytic%20models/schlick94b.pdf Schlick] (in the same paper where he described his BRDF model!), it can be written: | ||
| + | |||
| + | :<math>\mathrm{F}(\theta_d) = \mathrm{F}_0 + (1 - \mathrm{F}_0).(1 - \cos \theta_d)^5</math> | ||
| − | |||
The Fresnel reflection ''represents the increase in specular reflection as the light and view vectors move apart and predicts that all smooth surfaces will approach 100% specular reflection at grazing incidence''. | The Fresnel reflection ''represents the increase in specular reflection as the light and view vectors move apart and predicts that all smooth surfaces will approach 100% specular reflection at grazing incidence''. | ||
| Line 280: | Line 287: | ||
[[File:FresnelComparison.jpg]] | [[File:FresnelComparison.jpg]] | ||
| + | |||
Revision as of 22:42, 26 December 2012
Contents
Characteristics of a BRDF

Almost all the informations gathered here come from the reading and interpretation of the great Siggraph 2012 talk about physically based rendering in movie and game production [1] but I've also practically read the entire documentation about BRDFs from their first formulation by Nicodemus [2] in 1977!
So, what's a BRDF?
As I see it, it's an abstract tool that helps us to describe the macroscopic behavior of a material when photons hit this material. It's a convenient black box, a huge multi-dimensional lookup table (3, 4, or sometimes even 5, 6 dimensions when including spatial variations) that somehow encodes the amount of photons bouncing off the surface in a specific (outgoing) direction when coming from another specific (incoming) direction (and potentially, from another location).
It comes in many flavours
A Bidrectional Reflectance Distribution Function or BRDF is only a subset of the phenomena that happen when photons hit a material but there are plenty of other kinds of BxDFs:
- The BRDF only deals about reflection, so we're talking about photons coming from outside the material and scattered back to the outside the material as well.
- The BTDF (Transmittance) only deals about transmission of photons coming from outside the material and scattering inside the material (i.e. refraction).
- Note that the BRDF and BTDF only need to consider the upper or lower hemispheres of directions (which we call <math>\Omega</math>, or sometimes <math>\Omega_+</math> and <math>\Omega_-</math> if the distinction is required)
- The BSDF (Scattering) is the general term that encompasses both the BRDF and BTDF. This time, it considers the entire sphere of directions.
- Anyway, the BSDF, BRDF and BTDF are generally 4-dimensional as they make the (usually correct) assumption that both the incoming and outgoing rays interact with the material at a unique and same location.
- Also, the BSDF could be viewed as an incorrect term since it not only accounts for scattering but also for the other phenomenon happening to photons when they hit a material: absorption. This is because of absorption that the total integral of the BRDF for any outgoing direction is less than 1.
- The BSSRDF (Surface Scattering Reflectance) is a much larger model that also accounts for different locations for the incoming and outgoing rays. It thus becomes 5- or even 6-dimensional.
- This is an expensive but really important model when dealing with translucent materials (e.g. skin, marble, wax, milk, even plastic) where light diffuses through the surface to reappear at some other place.
- For skin rendering, it's an essential model otherwise your character will look dull and plastic, as was the case for a very long time in real-time computer graphics. Fortunately, there are many simplifications that one can use to remove 3 of the 6 original dimensions of the BSSRDF, but it's only recently that real-time methods were devised [3].
First, what's the color of a pixel?
Well, a pixel encodes what the eye or a CCD sensor is sensitive to: it's called radiance.
Radiance is the radiant flux of photons per unit area per unit solid angle and is written as <math>L(x,\omega)</math>. Its unit is the Watt per square meter per steradian (<math>W.m^{-2}.sr^{-1}</math>).
- <math>x</math> is the location where the radiance is evaluated, it's a 3D vector!
- <math>\omega</math> is the direction in which the radiance is evaluated, it's also a 3D vector but it's normalized so it can be written as a couple of spherical coordinates <math>\langle \phi,\theta \rangle</math>.
The radiant flux of photons –or simply flux– is basically the amount of photons/energy per amount of time.
And since we're considering a single CCD sensor element or a single photo-receptor in the back of the eye (e.g. cone):
- We only perceive that flux in a single location, hence the "per square meter". We need the flux flowing through an infinitesimal piece of surface (at least, the area of a rod or a cone, or the area of a single CCD sensor element).
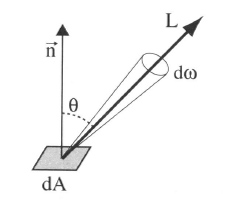
- We only perceive that flux in a single direction, hence the "per steradian". We need the flux flowing through an infinitesimal piece of the whole sphere of directions (or at least the solid angle <math>d\omega</math> covered by the cone or single CCD sensor element as shown in the figure below).
So the radiance is this: the amount of photons per seconds flowing along a ray of solid angle <math>d\omega</math> and reaching a small surface <math>dA</math>. And that's what is stored in the pixels of an image.
A good source of radiance is one of those HDR cube maps used for Image Based Lighting (IBL): each texel of the cube map represents a piece of the photon flux reaching the point at the center of the cube map. It encodes the entire light field around an object and if you use the cube map well, your object can seamlessly integrate into the real environment where the cube map photograph was taken (thanks to our dear Paul Debevec) (ever noticed how movies before 1999 had poor CGI? And since his paper on HDR probes, it's a real orgy! ![]() ).
).
But IBL is also very expensive: ideally, you would need to integrate each texel of the cube map and dot it with your normal and multiply it by some special function to obtain the perceived color of your surface in the view direction.
And guess what this special function is?
Well, yes! It's the BRDF and it's used to completely describe the behavior of radiance when it interacts with a material. Any material...
Mathematically
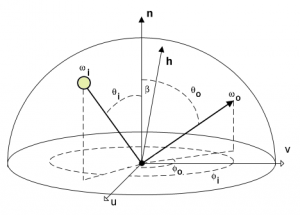
We're going to use <math>\omega_i</math> and <math>\omega_o</math> to denote the incoming and outgoing directions respectively. Each of these 2 directions are encoded in spherical coordinates by a couple of angles <math>\langle \phi_i,\theta_i \rangle</math> and <math>\langle \phi_o,\theta_o \rangle</math>. These only represent generic directions, we don't care if it's a view direction or light direction.
For example, for radiance estimates, the outgoing direction is usually the view direction while the incoming direction is the light direction. For importance estimates, it's the opposite.
Also note that we use vectors pointing toward the view or the light.
Irradiance
The integration of radiance arriving at a surface element <math>dA</math>, times <math>n.\omega_i</math> yields the irradiance (<math>W.m^{-2}</math>):
- <math>E_r(x) = \int_\Omega dE_i(x,\omega_i) = \int_\Omega L_i(x,\omega_i) (n.\omega_i) \, d\omega_i~~~~~~~~~\mbox{(1)}</math>
It means that by summing the radiance (<math>W.m^{-2}.sr^{-1}</math>) coming from all possible directions, we get rid of the angular component (the <math>sr^{-1}</math> part).
Irradiance is the energy per unit surface (when leaving the surface, the irradiance is then called radiosity, I suppose you've heard of it). It's not very useful because, as we saw earlier, what we need for our pixels is the radiance.
Intuitively, we can imagine that we need to multiply that quantity by a value that will yield back a radiance. This mysterious value has the units of per steradian (<math>sr^{-1}</math>) and it's indeed the BRDF.
First try
So, perhaps we could include the BRDF in front of the irradiance integral and obtain a radiance like this:
- <math>L_r(x,\omega_o) = f_r(x,\omega_o) \int_\Omega L_i(\omega_i) (n.\omega_i) \, d\omega_i</math>
Well, it can work for a few cases. For example, in the case of a perfectly diffuse reflector (Lambert model) then the BRDF is a simple constant <math>f_r(x,\omega_o) = \frac{\rho(x)}{\pi}</math> where <math>\rho(x)</math> is called the reflectance (or albedo) of the surface. The division by <math>\pi</math> is here to account for our "per steradian" need.
This is okay as long as we don't want to model materials that behave in a more complex manner. Most materials certainly don't handle incoming radiance uniformly, without accounting for the incoming direction! They must redistribute radiance in some special and strange ways...
For example:
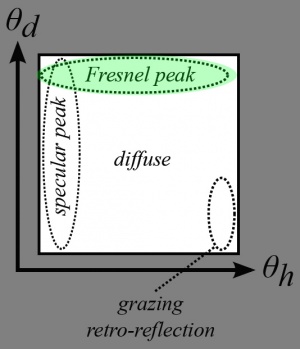
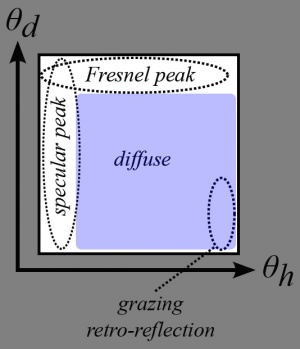
- Many materials have a specular peak: a strong reflection of photons that tend to bounce off the surface almost in the direction perfectly symmetrical to the incoming direction (your average mirror does that).
- Also, many rough materials imply a Fresnel peak: a strong reflection of photons that arrive at the surface with glancing angles (fabrics are a good example of Fresnel effect)
That makes us realize the BRDF actually needs to be inside the integral and become dependent on the incoming direction <math>\omega_i</math> as well!
The actual formulation
When we inject the BRDF into the integral, we obtain a new radiance:
- <math>L_r(x,\omega_o) = \int_\Omega f_r(x,\omega_o,\omega_i) L_i(\omega_i) (n.\omega_i) \, d\omega_i~~~~~~~~~\mbox{(2)}</math>
We see that now <math>f_r(x,\omega_o,\omega_i)</math> is dependent on both <math>\omega_i</math> and <math>\omega_o</math> and becomes much more difficult to handle than our simple Lambertian factor from earlier.
Anyway, we now integrate radiance multiplied by the BRDF. We saw from equation (1) that integrating without multiplying by the BRDF yields the irradiance, but when integrating with the multiplication by the BRDF, we obtain radiance so it's perfectly reasonable to assume that the expression of the BRDF is:
- <math>f_r(x,\omega_o,\omega_i) = \frac{dL_r(x,\omega_o)}{dE_i(x,\omega_i)}~~~~~~~~~~~~\mbox{(which is simply radiance divided by irradiance)}</math>
From equation (1) we find that:
- <math>dE_i(x,\omega_i) = L_i(x,\omega_i) (n.\omega_i) d\omega_i~~~~~~~~~~~~\mbox{(note that we simply removed the integral signs to get this)}</math>
We can then finally rewrite the true expression of the BRDF as:
<math>f_r(x,\omega_o,\omega_i) = \frac{dL_r(x,\omega_o)}{L_i(x,\omega_i) (n.\omega_i) d\omega_i}~~~~~~~~~\mbox{(3)}</math>
The BRDF can then be seen as the infinitesimal amount of reflected radiance (<math>W.m^{-2}.sr^{-1}</math>) by the infinitesimal amount of incoming irradiance (<math>W.m^{-2}</math>) and thus has the final units of <math>sr^{-1}</math>.
Physically
To be physically plausible, the fundamental characteristics of a real material BRDF are:
- Positivity, any <math>f_r(x,\omega_o,\omega_i) \ge 0</math>
- Reciprocity (a.k.a. Helmholtz principle), guaranteeing the BRDF returns the same value if <math>\omega_o</math> and <math>\omega_i</math> are reversed (i.e. view is swapped with light). It means that <math>f_r(x,\omega_o,\omega_i) = f_r(x,\omega_i,\omega_o)</math>
- Energy conservation, guaranteeing the total amount of reflected light is less or equal to the amount of incoming light. In other terms: <math>\forall\omega_o \int_\Omega f_r(x,\omega_o,\omega_i) (n.\omega_i) \, d\omega_i \le 1</math>
Although positivity and reciprocity are usually quite easy to ensure in physical or analytical BRDF models, energy conservation on the other hand is the most difficult to enforce!
BRDF Models
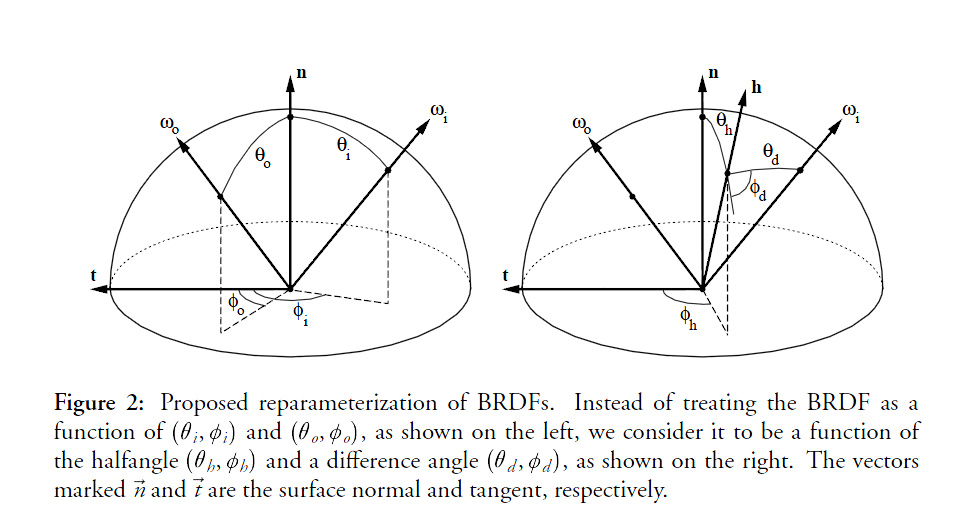
Before we delve into the mysteries of materials modeling, you should get yourself familiar with a very common change in variables introduced by Szymon Rusinkiewicz [4] in 1998.
The idea is to center the hemisphere of directions about the half vector <math>h=\frac{\omega_i+\omega_o}{\left \Vert \omega_i+\omega_o \right \|}</math> as shown in the figure below:
This may seem daunting at first but it's quite easy to visualize with time: just imagine you're only dealing with the half vector and the incoming light vector (or the outgoing view vector, we don't care since they're interchangeable).
- The orientation of the half vector <math>h</math> is given by 2 angles <math>\langle \phi_h,\theta_h \rangle</math>. These 2 angles tell us how to rotate the original hemisphere aligned on the surface's normal <math>n</math> so that now the normal coincides with the half vector: they define <math>h</math> as the new north pole.
- Finally, the direction of the incoming vector <math>\omega_i</math> is given by 2 more angles <math>\langle \phi_d,\theta_d \rangle</math> defined on the new hemisphere aligned on <math>h</math>.
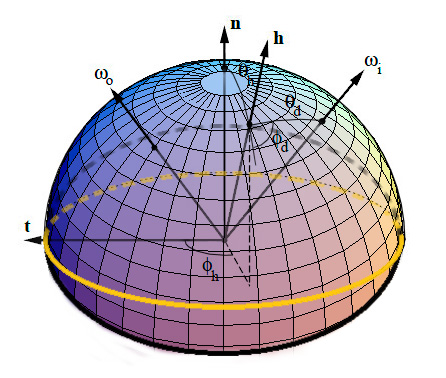
Here's an attempt at a figure showing the change of variables:
We see that the inconvenience of this change is that, as soon as we get away from the normal direction, a part of the new hemisphere stands below the material's surface (represented by the yellow perimeter). It's especially true for grazing angles when <math>h</math> is at 90° off of the <math>n</math> axis: half of the hemisphere stands below the surface!
The main advantage though, is when the materials are isotropic then <math>\phi_h</math> has no significance for the BRDF (all viewing azimuths yield the same value) so we need only account for 3 dimensions instead of 4, thus significantly reducing the amount of data to store!
BRDF From Actual Materials
Before writing about analytical and artificial models, let's review the existing physical measurements of BRDF.
There are few existing databases of material BRDFs, we can think of the MIT CSAIL database containing a few anisotropic BRDF files but mainly, the most interesting database of isotropic BRDFs is the MERL database from Mitsubishi, containing 100 materials with many different characteristics (a.k.a. the "MERL 100").
50 of these materials are considered "smooth" (e.g. metals and plastics) while the remaining 50 are considered "rough" (e.g. fabrics).
Source code is provided to read back the BRDF file format. Basically, each BRDF is 33MB and represents 90x90x180 RGB values stored as double precision floating point values (90*90*180*3*sizeof(double) = 34992000 = 33MB).
The 90x90x180 values represent the 3 dimensions of the BRDF table, each dimension being <math>\theta_h \in [0,\frac{\pi}{2}]</math> the half-angle off from the normal to the surface, <math>\theta_d \in [0,\frac{\pi}{2}]</math> and <math>\phi_d \in [0,\pi]</math> the difference angles used to locate the incoming direction. As discussed earlier, since we're considering isotropic materials, there is no need to store values in 4 dimensions and the <math>\phi_h</math> can be safely ignored, thus saving a lot of room!
I wanted to speak of actual materials and especially of the Disney BRDF Viewer first because they introduce a very interesting way of viewing the data present in the MERL BRDF tables.
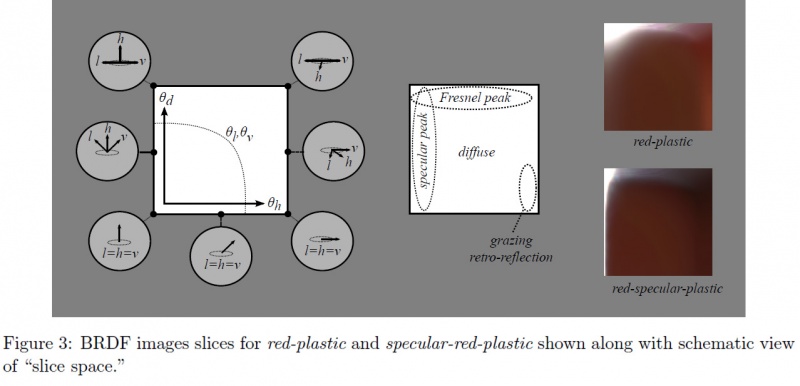
Indeed, one way of viewing the 3D MERL table is to consider a stack of 180 slices (along <math>\phi_d</math>), each slice being 90x90 (along <math>\theta_d</math> and <math>\theta_h</math>).
This is what the slices look like when we make <math>\phi_d</math> change from 0 to 90°:
We can immediately notice the most interesting slice is the one at <math>\phi_d = \frac{\pi}{2}</math>. We also can assume the other slices are just a warping of this unique, characteristic slice but we'll come back to that later.
Another thing we notice with slices with <math>\phi_d \ne \frac{\pi}{2}</math> are the black texels. Remember the change of variables we discussed earlier? I told you the problem with this change is that part of the tilted hemisphere lies below the surface of the material. Well, these black texels represent directions that are below the surface. We see it gets worse for <math>\phi_d = 0</math> where almost half of the table contains invalid directions. And indeed, the MERL database's BRDF contain a lot (!!) of invalid data. In fact, 40% of the table is useless, which is a shame for files that each weigh 33MB. Some effort could have been made from the Mitsubishi team to create a compressed format that discards useless angles, saving us a lot of space and bandwidth... Anyway, we're very grateful these guys made their database public in the first place! ![]()
So, from now on we're going to ignore the other slices and only concentrate on the characteristic slice at <math>\phi_d = \frac{\pi}{2}</math>.
Here is what the "MERL 100" look like when viewing only their characteristic slices:
Now let's have a closer look at one of these slices:
Talk about spec/fresnel/diffuse/backlighting zones.
Analytical models of BRDF
There are many (!!) available models:
- Phong (1975)
- Blinn-Phong (1977)
- Cook-Torrance (1981)
- Ward (1992)
- Oren-Nayar (1994)
- Schlick (1994)
- Modified-Phong (Lafortune 1994)
- Lafortune (1997)
- Neumann-Neumann (1999)
- Albedo pump-up (Neumann-Neumann 1999)
- Ashikhmin-Shirley (2000)
- Kelemen (2001)
- Halfway Vector Disk (Edwards 2006)
- GGX (Walter 2007)
- Distribution-based BRDF (Ashikmin 2007)
- Kurt (2010)
- etc.
Each one of these models attempt to re-create the various parts of the characteristic slices we saw earlier with the MERL database, but none of them successfully covers all the parts of the BRDF correctly.
The general analytical model that is often used by the models listed above is called "microfacet model". It is written like this for isotropic materials:
- <math>f_r(x,\omega_o,\omega_i) = \mbox{diffuse} + \mbox{specular} = \mbox{diffuse} + \frac{F(\theta_d)G(\theta_i,\theta_o)D(\theta_h)}{4\cos\theta_i\cos\theta_o}</math>
Specularity
This "simple" model makes the assumption a macroscopic surface is composed of many perfectly specular microscopic facets, a certain amount of them having their normal <math>m</math> aligned with <math>h</math>, making them good candidates for specular reflection and adding their contribution to the outgoing radiance. This distribution of normals in the microfacets is given by the <math>D(\theta_h)</math> also called Normal Distribution Function or NDF.
The NDF is here to represent the specularity of the BRDF but also the retro-reflection at glancing angles. There are many models of NDF, the most well known being the Blinn-Phong model <math>D_\mathrm{phong}(\theta_r) = \frac{2+n}{2\pi} \cos\theta_h^n</math> where n is the specular power of the Phong lobe.
We can also notice the Beckmann distribution <math>D_\mathrm{beckmann}(\theta_h) = \frac{\exp{\left(-\tan^2(\theta_h)/m^2\right)}}{\pi m^2 \cos^4(\theta_h)}</math> where m is the Root Mean Square (rms) slope of the surface microfacets (the roughness of the material).
Another interesting model is the Trowbridge-Reitz distribution <math>D_\mathrm{TR}(\theta_h) = \frac{\alpha_\mathrm{tr}^2}{\pi(\alpha_\mathrm{tr}^2.\cos(\theta_h)^2 + sin(\theta_h)^2)}</math>
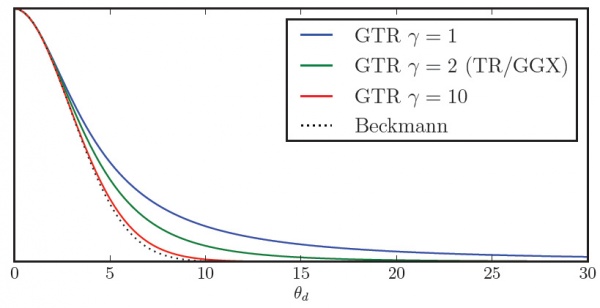
Most models fail to accurately represent specularity due to "short tails" as can be seen in the figure below:
Disney uses an interesting variation of the Trowbridge-Reitz distribution that helps to compensate for the short tail problem:
- <math>D_\mathrm{generalizedTR}(\theta_h) = \frac{\alpha_\mathrm{tr}^2}{\pi(\alpha_\mathrm{tr}^2.\cos(\theta_h)^2 + sin(\theta_h)^2)^\gamma}</math>
You can find more interesting comparisons of the various NDF in the talk by Naty Hoffman.
Shadowing
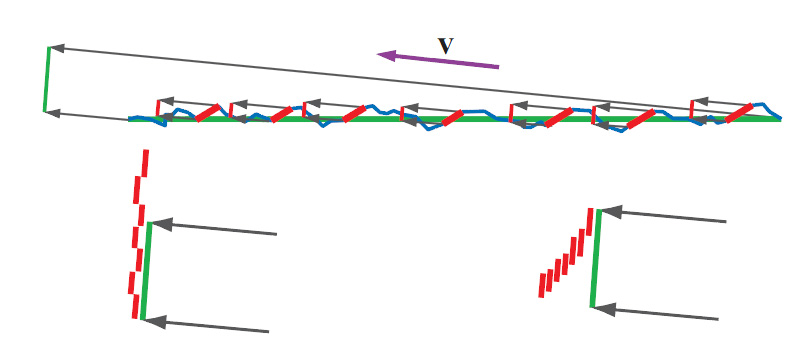
Continuing with the micro facet model, because the landscape of microfacets is not perfectly flat, some of the micro facets will shadow or mask other facets. This is the geometric factor represented by the <math>G(\theta_i,\theta_o)</math> term.
This geometric factor is usually quite hard to get but is essential to the energy-conservation problem otherwise, the micro-facets model can easily output more energy than came in, especially at glancing angles as shown on the figure below:
The top figure shows a very slant view direction. The micro-facets contributing to the lighting in the view direction (regardless of shadowing) are highlighted in red. In the bottom row, the projection of the surface area in the view direction is represented as the green line. The bottom left figure shows an incorrect accumulation of the total area of micro facets where shadowing is not accounted for, resulting in a total reflection surface larger than the projected surface which will yield more energy than actually incoming to the surface area. The bottom right shows correct accumulation of the total area that takes shadowing into account, the resulting area is smaller than the projected surface area and cannot reflect more energy than put in.
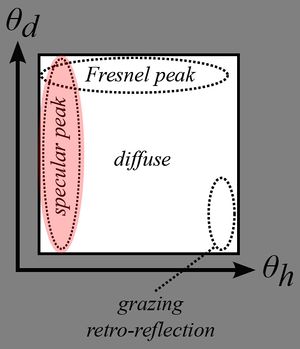
Fresnel
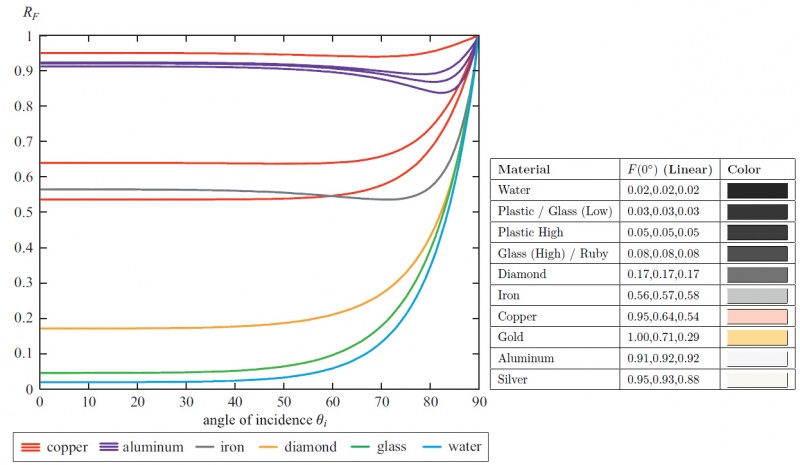
The <math>F(\theta_d)</math> term is called the "Fresnel Reflectance" and models the amount of light that will effectively participate to the specular reflection (the rest of the incoming light entering the surface to participate to the diffuse effect).
We immediately notice that:
- The Fresnel reflectance curves don't change much over most of the range, say from 0° (i.e. light/view is orthogonal to the surface) to ~60°, then the reflectance jumps to 1 (i.e. total reflection) at 90° which is quite intuitive since photons arriving at grazing angles have almost no chance of entering the material and almost all of them bounce off the surface. The Fresnel reflectance value when <math>\theta_d = 0°</math> (i.e. when viewing the surface perpendicularly) is called <math>F_0</math> and is often used as the characteristic specular reflectance of the material. It's very convenient as it can be represented by a RGB color in [0,1] and we can think of it as the "specular color" of the material.
- Metals usually have a colored specular reflection while dielectric materials (e.g. water, glass) have a uniform specular and need only luminance encoding.
- Finally, we can notice (actually, I didn't notice that at all, I read it in one of the lectures
 ) that smooth materials generally have a Fresnel reflectance <math>F_0 < 0.5</math> while rough materials have a <math>F_0 > 0.5</math>.
) that smooth materials generally have a Fresnel reflectance <math>F_0 < 0.5</math> while rough materials have a <math>F_0 > 0.5</math>.
The expressions for the Fresnel reflectance are quite complicated and deal with complex numbers but thanks to a simplification by Schlick (in the same paper where he described his BRDF model!), it can be written:
- <math>\mathrm{F}(\theta_d) = \mathrm{F}_0 + (1 - \mathrm{F}_0).(1 - \cos \theta_d)^5</math>
The Fresnel reflection represents the increase in specular reflection as the light and view vectors move apart and predicts that all smooth surfaces will approach 100% specular reflection at grazing incidence.
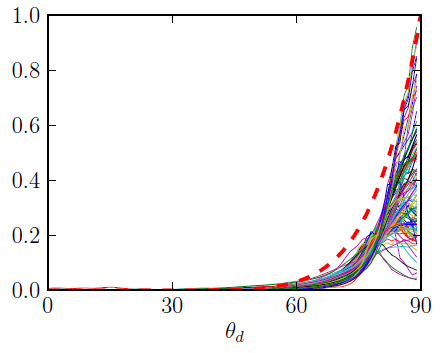
This is purely theoretical though, because in reality many materials don't reflect light as predicted by the Fresnel function as can be seen in the figure below where the theoretical Fresnel reflection is compared to the reflection 100 MERL materials at grazing incidence:
rough materials => coefficients < 0.5 smooth materials => > 0.5
Diffuse Part
The diffuse part of the equation is modeled by diffuse models like Lambert, Oren-Nayar or Hanrahan-Krueger:
To conserve energy, the diffuse part should also be multiplied by the factor giving the percentile of energy that remains after having been specularly reflected. The simplest choice would be to use <math>1 - F(\theta_h)</math> but more complex and accurate models exist (TODO).
Retro-Reflection is often related to material roughness
From "Background: Physics and Math of Shading (Naty Hoffman)" I learned that:
- metals completely absorb photons if they are not reflected specularly: metals have no diffuse components.
- Moreover, metals usually have a colored specular (due to RGB variations in the Fresnel reflections) while dielectric materials have a uniform specular and need only luminance encoding.
It's clearly visible with image slices of metal BRDFs:
[[File:]]
Lafortune lobes!
What can we bring to the table?
References
[1] [http://blog.selfshadow.com/publications/s2012-shading-course/ "Practical Physically Based Shading in Film and Game Production" Siggraph 2012 talk.
[2] "Geometrical Considerations and Nomenclature for Reflectance" F.E. Nicodemus et al. 1977
[3] "Screen-Space Perceptual Rendering of Human Skin" Jimenez et al. (2009)
[4] "A New Change of Variables for Efficient BRDF Representation" Szymon Rusinkiewicz (1998)